Griffiths, Introduction to electrodynamics, in problem 12, shows that if a man starts running at moment $t=0$ from position $x>0$, under the influence of a constant force, will never be reached by a light ray that passes at the origin at time $t>0$.
Shown in the picture is the man as the hyperbolic line, photons as dashed lined -
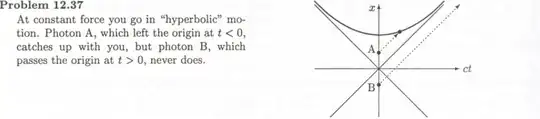 The picture is of course pretty clear and it is obvious the man and the ray will never cross paths because they are separated by the trajectory of another.
The picture is of course pretty clear and it is obvious the man and the ray will never cross paths because they are separated by the trajectory of another.
But on the other hand, the man of course sees the light and the light will always travel faster the him, so how come the light will never reach him?