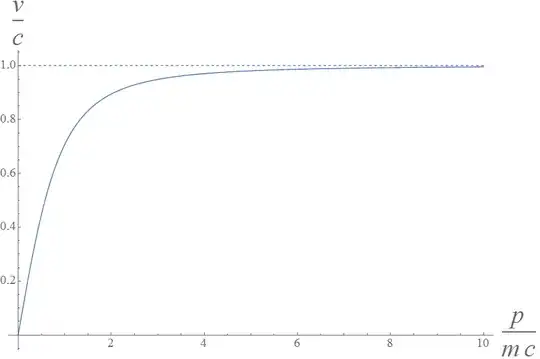
Neutrinos always travel at same speed?

Question

Neutrinos have mass, and only interact with gravitional and weak force, what make it very difficult to detect.

Neutrinos is known to travel very closer to speed of light and have very small mass altought neither have a precise measure.

Particles with no mass like photons and gluons (altought there is no free gluon) must travel at speed of light (vacuum).

Particles that have mass must travel in any velocity lower than speed of light.

Dark matter can have hot particles (near speed of light) and cold particles (non relativistic velocity).

My questions are:

1. Does neutrinos have always the same velocity?

2. Is it possible to have neutrinos travelling with non-relativistic speeds?

3. Why only referred neutrinos as possible hot dark matter and not to cold dark matter?

Answer 1

It is known, through the observation of the phenomenon of flavor oscillations, that neutrinos definitely have nonzero mass.

Therefore there's a definite answer to your answer: neutrinos most assuredly do not always travel at the same speed.

Probably what is causing you to have doubts is that neutrinos aren't observed to have speeds other than $c$, to within experimental error. So what's going on?

It is instructive to plot the momentum four-vector norm equation $E^2/c^2-p^2 = m^2 c^2$ for a particle in normalized co-ordinates so that it shows normalized speed $\frac{v}{c}$ against normalized momentum $\tilde{p} = \frac{p}{m\,c}$:

There is always behavior like this: for very massive particles, the region where $v$ differs significantly from $c$ is wide: for very light particles, the same region is very concentrated around $p=0$, but its the same shapen curve, just stretched or shrunken in $p$-scale. More details in my answer here.

We see therefore that for a particle with a very low rest mass, such as a neutrino, the momentum has to be very small to observe the particle at a speed less than $c$. However, this means a particle with an impossibly long wavelength, which means it is very hard to prepare in such a state, and a neutral particle without much momentum will not trigger detection events. So, from a practical point of view, the particle becomes almost impossible to observe at a speed very different from $c$: the conditions whereunder it has different motion make it "invisible".

Answer 2

It is possible for neutrinos to have non relativistic velocities. There is no reason why that shouldn't be the case because velocity depends on the frame of reference of the observer.

They also can change their velocity due to the gravitational field for example.

Answer 3

We can start this off best, if we take a look at the relativistic relationship between total energy $E$, rest mass $m_\nu$ and momentum $p$:
$E^2 = m_\nu^2 + p^2 $ (in natural units of SR)
Since momentum is a kind of a measure for velocity (since rest mass is fixed), we formulate this as $p = \sqrt{E^2 + m_\nu^2}$
So the velocity of a particle is obviously dependent on the energy with which the particle is created. If you now take a look on your average solar neutrino with about 10 MeV, you will notice really quickly that kinetic energy does not differ so much from total energy if a neutrino mass is $m_\nu < 1$ eV. Therefore almost all energy is kinetic energy, which leads to ultra-relativistic velocities.

Answer 4

The 25 detected neutrinos from supernova 1987A--168,000 light years away--arrived over a span of 13 seconds [Wikipedia, which is never wrong]. Not all neutrinos are this energetic, though.