1

The centrifugal force causes a distension at the equator. With a simple model we can estimate the dimension of this deformation ellipsoid. We start with a mass $m$ at the point $P$ on the surface of the deformed earth at the height $h$ over the non-deformed earth.

Assume all particles are in balanced state on the surface. Show that the height of the particle can be described as: $$h = \frac{R^2\omega^2}{6g}(3sin^2 \theta-2).$$

I received some tips how to approach this problem: $$U_{total} = mgh - \frac{m}{2}\omega^2x^2 + C$$ Determine h out of the potential energy, when the particle is in balance.

Use spherical coordinates.

Assume the volume of the deformed earth is the same as the volume of the non deformed earth.

Integrate over the spherical surface.(that's the thing I don't understandt)

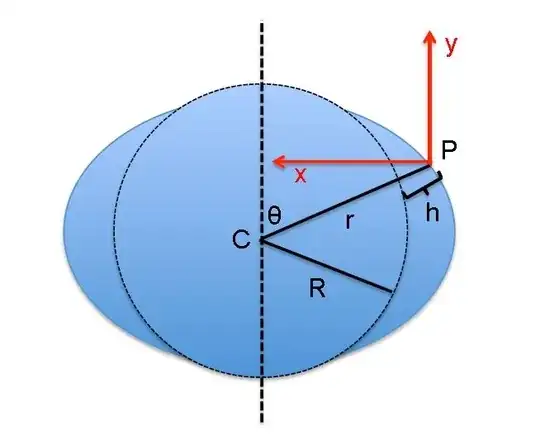
Here's a picture of the problem: Task-Deformation

first step is easy: $$mgh = \frac{m}{2}\omega^2x^2 + C$$ with $x=r*sin(\theta)$ $$h=\frac{\omega^2R^2sin^2(\theta)}{2g} + B$$ with $B = -C/mg$.

From this point on I don't understand how to keep processing. We have solved for $h$. Why do I need to integrate? And far more confusing, why integrating over the spherical surface?! What's the principle behind this?

Community
  • 1
the_asdf_word
  • 29

1 Answers1

1

In your comments in your answer to @Floris, you are doing the integral wrong. The volume element is $dV=r^2\sin\theta\,\mathrm dr\,\mathrm d\theta\,\mathrm d\phi$ but because $r=R+h\approx R$, you can approximate (after taking the radial integral and azimuthal integrals) it as $2\pi R^2h\sin\theta\,\mathrm d\theta$. You were missing that factor of $\sin\theta$. Using $A=\frac{\omega^2R^2}{2g}$,

$$\int_0^\pi (A\sin^2\theta+B)\sin\theta\,\mathrm d\theta=\frac{4}{3}A+2B$$

The difference in volume from a sphere is therefore $4\pi R^2\left(\frac{\omega^2R^2}{3g}+B\right)$. Setting that equal to $0$ gets you a value of $-\frac{\omega^2R^2}{3g}$ for $B$, which is the result you're looking for.

Johnathan Gross
  • 1,849