The wormhole is a modification of spacetime, and not necessarily that connected to a black hole, where by some "magic" there is more space in a region then ordinarily would be. A case of this odd situation with space is to have two disks of paper where you cut a wedge out of one of them and then glue that wedge into a radial region of the other disk. The first disk is a cone and the second has an odd "floppy" appearance. The first of these if we can smooth out the point on the cone is a dome or part of a sphere while the disk with excess area is a saddle shap once we iron out all the excess area evently through the thing. We are robbing Peter to pay Paul so to speak by taking space from one disk and putting it in the other. The spherical cap or dome has positive curvature and the saddle shaped 2-dimensional space has negative curvature.
The metric for flat Minkowski spacetime is
$$
ds^2~=~dt^2~-~dr^2~-~r^2(d\theta^2~+~sin^2\theta d\phi^2),
$$
and we can modify this to make the Morris-Thorne wormhole with line element
$$
ds^2~=~dt^2~-~dr^2~-~(r^2~+~\rho^2)(d\theta^2~+~sin^2\theta d\phi^2).
$$
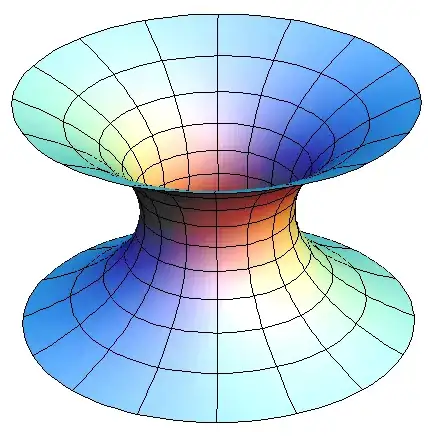
Here $\rho$ is the radius of the throat or minimum radius of the bell of the hyperboloid. This add additional surface area to the $2$ sphere defined by $r^2(d\theta^2~+~sin^2\theta d\phi^2)$ with the throad radius $\rho$. So a foliation of two-surfaces making three dimensional space has an appearance in a 2 dimensional projection as the catenoid seen below.
The connection terms are rather odd in a way. For instance two of them are
$$
\Gamma^\theta_{r\theta r}~=~\Gamma^\phi_{r\phi r}~=~\frac{r}{r^2~+~\rho^2},
$$
Where one can derive geodesic equation with an acceleration in the $\theta$ and $\phi$ directions. The curvatures are
$$
R_{r\theta r\theta}~=~-\frac{\rho^2}{r^2~+~\rho^2},~R_{r\phi r\phi}~=~-\frac{\rho^2sin^2\theta}{r^2~+~\rho^2},~R_{\theta\phi\theta\phi}~=~\rho sin^2\theta.
$$
These strange $\theta$ and $\phi$ dependent curvatures are saying there is this negative curvature by “cramming more space” into this region. This negative curvature is what is induced by so called exotic matter.
How does this connect to black holes? We can now modify this model so that
$$
ds^2~=~\left(1~-~\frac{2m}{r}\right)dt^2~-~\left(1~-~\frac{2m}{r}\right)^{-1}dr^2~-~(r^2~+~\rho^2)(d\theta^2~+~sin^2\theta d\phi^2).
$$
If we identify the event horizon with the throat radius of the wormhole then $\rho~=~2m$, and sometimes we have $\rho~=~2m~+~\delta r$ which permits an entering particle to avoid the event horizon. A physically more realistic situation might be where $\rho~<~2m$ so the wormhole throat is inside the black hole. In that way an observer can only wormhole around inside the black hole without causing unfortunate “issues” of chronology and causality in the outside world. We think of this black hole as having been laced with this exotic matter. If this stuff falls towards the black hole is reaches a certain density near the horizon as seen by a distant observer and its negative energy and negative curvature adjusts the structure of the black hole.