If you spin a single nucleus containing multiple nucleons fast enough it will fly apart.
Is there a speed limit to a spinning proton or electron assuming it's held at a fixed location with a strong magnetic field?
What speed would either have to attain before breaking up, assuming they can be broken up? What would they break up into?
You can't spin up an electron. The only way that is possible is if as a string you can put angular momentum on it that way. The energy required to do that would be near Planck scale energy. So I will say this is not possible with the electron FAPP.
For the proton you can spin it up. This is the Regge trajectory that has the angular momentum $J$ as the abscissa and $M^2$as the ordinate. At the bottom here is the $940MeV$ particle, corresponding to the proton. The proton is made of three quarks and they have intrinsic spin $\frac{\hbar}{2}$ that adds up to the same. If I spin this up, we think of these three quarks as being like the masses on a bolos the Argentine gauchos use to rope cattle. The next higher state has a mass of $1680MeV$. This state is not stable and the additional $740MeV$ of rest mass can enter into the production of mesons. We may think of the proton with $udd$ quarks such that one of the $d$ quarks has its "gluon string" break so it becomes coupled to a $d$ anti-quark and the $d$ quark remains with the baryon. the $d,\bar d$ meson carries off this additional mass energy.
For a whole nucleus you have similar physics, though a bit more complicated. There are people who work with rotating nuclei.
How fast can you spin a proton or electron without breaking it?
Even in the link you give, spin is a quantum number which can increase if the energy input to the nucleus is increased, the individual nuclei going to higher energy bound states ( or quantum mechanically defined bands) in higher angular momentum quantum numbers.
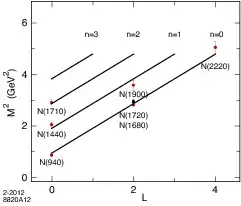
A proton is composed out of quarks. When enough energy is supplied to the proton the quarks settle at higher energy states with higher angular momentum. These are called baryonic resonances and are, as stated in the comments by Jonathan Gross, and can have spins higher than 1/2 of the proton neutron. The energies are of order of Mev, the delta resonance, spin 3/2, is about 200 MeV heavier than the proton and energy has to be supplied in the scattering process higher than that order of magnitude.
The electron is an elementary particle , a point particle , in the very well validated standard model of particle physics. It has an intrinsic spin but it is not a composite , but a point particle. It cannot be "broken up".
