Fields scale as $M/r^2$, so scaling a structure's dimensions up by $\alpha$ and decreasing its mass density by $\alpha$ leaves the field unchanged. So the field at the center of a cylinder whose diameter increases linearly along its length (I initially incorrectly suggested exponential) and whose mass-density is decreasing inversely with length will have the same constant non-zero field everywhere along its length.
A linear change with length means, of course, that its a simple cone. We can expand the angle at the vertex until the cone becomes a sphere. So if you take a planet with a hole through the middle that happens to have a mass density inversely proportional to radius, then the field will be constant and reverse sign at the center. In fact, the hole doesn't have to go through the middle. The field everywhere has a constant magnitude, only its angle changes. Actually I read somewhere that the earth's density has a slight tendency towards a 1/r dependence and the field in the first 1000 miles or so doesn't change much, but I don't have a reference.
If we talk about a conical shell then the area mass density has to be constant for the constant field scaling to apply. So next time you eat an ice cream cone please be aware that its gravitational field along its axis is roughly constant.
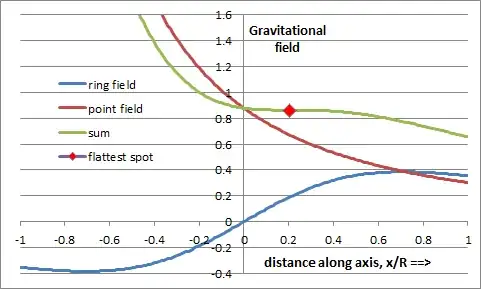
Thinking of a simple structure more analagous to the Helmholz configuration, the field along the axis of a ring radius R goes as $GMx/(R^2+x^2)^{3/2}$. If we place the point mass, $m$, on the axis at distance, $d$, from the ring, the total field is $GMx/(R^2+x^2)^{3/2} + Gm/(x-d)^2$. We can now choose $m$ and $d$ and a position $p$ to set the first, second, and third derivatives to zero. I had to solve this numerically. The answer comes out to be m/M = 1.75620, d/R = -1.41456, p/R = 0.202622. The resulting field is 0.862275*GM/R^2