Does pure yellow exist in variations we can't discern?

Question

If you add red light (~440 THz) and green light (~560 THz), you get what we perceive as yellow light (~520 THz). But I assume what you really get is a mixed waveform that we perceive as yellow? Suppose the red is a perfect sine wave, and so is the green, the mix of both will not be a perfect sine wave but a wobbly composite thing - right? Which is different than a perfect sine wave of ~520 THz. But we call both things "pure" yellow. Is that correct?

If so, are there animals that can discern composite pure yellow from singular pure yellow, like we can discern the mixture of multiple audio sine waves as a chord? Or is there machinery that can do that?

See also: Why both yellow and purple light could be made by a mix of red, green and blue?

Answer 1

Our ability to separate different colors from each others depends crucially on how many different receptors we have for colored light.

Humans have three different receptors for light, which means that we can characterize colors by three numbers, just like the RGB-codes of colors on your screen.

At the end of the day, what determines with colors we perceive is how the wave-form is projected onto these three numbers. Since there is an infinite set of wave forms, there is an infinite mixture of colors that we will perceive as identical (for every perceived color).

Some animals have more than three types of color receptors, and can therefore distinguish more wave-forms of light. You can say that their color perception is higher dimensional (4D,5D,... etc) than our 3 dimensional color perception.

Answer 2

Mikael Fremling's answer is excellent, but here is just a little more detail:

The light that hits your eye is a mixture of many different pure wave lengths, all at different intensities.

The red sensor in your eye computes the weighted average of those intensities, with weights that are concentrated around 440thz. The green sensor computes a different weighted average, with weights concentrated around 560thz, etc. (This is a stylized example; they're surely concentrated near some other wave lengths, not exactly 440 and 560.)

Each type of sensor computes one number. Your brain interprets those three numbers as a color.

There are many different combinations of intensities that all produce the same three weighted averages and therefore all look identical to your brain.

Answer 3

The answers here are correct, but have not answered your question about whether other animals can detect such a "pure" color.

The first tricky part of this is that there is no way to observe a "pure sine wave" as a single frequency. If you want to know the math, you can investigate Fourier transforms, but basically the mere fact that you cannot observe the signal for an indefinite period of time actually forces the tiniest smearing of the frequencies. This effect is far smaller than other factors like noise, but I point it out because it shows that it is mathematically impossible to observe a single frequency of light. You must always observe a band. And, in fact, that band must have some sensitivity at all frequencies. That's just the math. We can talk about a reasonably pure sine wave, but there are mathematical limits that prevent us from every observing something perfectly.

With that in mind, we can talk about whether there is a creature which can observe the band of "yellows." 510-540THz is a typical range of frequencies that we may assign a "yellow" color (actual ranges depend on personal perceptions, which are way beyond the scope of this question). So you might ask if there is an animal that can recognize 510-540THz sine waves, and distinguish them from a mixture of red and green that you and I might interpret as yellow because we are trichromats.

As it turns out, there is such a creature! It is the Mantis Shrimp. The mantis shrimp has sensors which are sensitive to 16 different bands, rather than our measly 3. However, the linked Oatmeal comic misses out on an interesting limitation of the Mantis Shrimp. Studies have shown that the Mantis Shrimp doesn't actually have all that good of color perception. Unlike us, it doesn't process the colors together. It doesn't take the reds and greens and figure out how yellowish the object is. Instead, each color band is processed independently.

While this means the Mantis Shrimp can't see color as well as we can, it does mean its style of vision is an exact match for what you want: sensitivity to a band of frequencies.

Answer 4

As an add-on to the existing (excellent) answers, to address the last point in your question,

Or is there machinery that can do that?

the answer is yes: they're known as spectrometers, and they let you split the light into its component colours up to very high resolutions, giving you output that looks something like this:

^{Image source}

Spectrometers can be very complicated machines, but for simple examples you can just use a triangular glass prism or even a blank CD as a diffraction grating $-$ and, indeed, the source for the image above has a nice tutorial for how to build a DIY spectrometer at home, which will show very clear differences between e.g. clandlelight vs LED-based flashlights vs incandescent light sources.

Answer 5

Light is infinite dimensional (up to quantum fuzziness).

The number of photons of each frequency of light is independent of the photons of other frequencies of light, even ones the smallest distance away.

Our ability to sense light is based on (usually) a three pigment system in our eyes (some humans have 4, some have 2 and some have 1 or 0). These three pigments, plus our brain, map this infinite dimensional space into a 3 dimensional one.

When we see "pure red" plus "pure green" looks like "yellow", this means that when we excite the pigments in our eye with "red" and "green" photons in equal amounts, the result is the same as if we excited the pigments with "yellow" photons.

The "red" and "green" photons never become yellow photons. Your inability to distinguish red+green from yellow is in effect an optical illusion caused by limitations in how you see.

A creature with certain kinds of different, or more, pigments would not confuse "red+green" and "yellow"; the two might look completely different.

Because of how we sense light, there are colors we can see that do not correspond to any single frequency of light. There are no "brown" photons, nor are there "white" photons. These correspond to certain mixtures of photons in the 3 dimensional projection of the infinite dimensional color space that is real light.

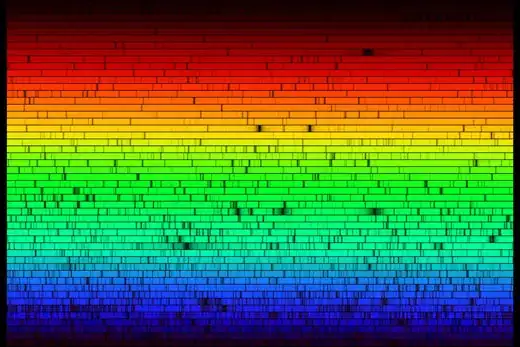
There are tools that let us distinguish between "red+green" and "yellow" light. The easiest is a prism -- each photon of light will be bent differently from it, so a narrow point-source of "yellow photons" will bend together, while "red+green" will be split apart by the prism.

Note that this doesn't match your art class colour mixture. Paint mixes via subtraction (each pigment absorbs certain colours and reflects the rest, and when you mix two both of their absorbtion occurs to some extent).

Photons or light mix by addition.

A big difference is that if you mix all your pigments together, you get a muddy brown or black (mixing many pigments can violate the region where the "absorbtion combines" approximation works, preventing it from being black). If you mix all your lights together, you get white (assuming they are in the right balance).

Answer 6

To the question "are there animals that can discern composite pure yellow from singular pure yellow":

Yes. Humans (who wear glasses). I first realized I could look through the edge of my glasses (and thus through an ad hoc prism) at spectra containing "purple" and distinguish between violet (405 nm (about 740 THz) from a laser diode) and red+blue = purple spectra. The laser diode has a spectral width of about 1 nm (corresponding to about 2 THz), so is a relatively pure real source of light. The red + blue were various organic fluorophores, so were not nearly as spectrally pure.

There's nothing special about "purple" in this story. This would work just fine for yellow versus red + green = yellow.