2

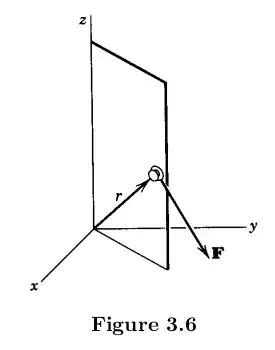
I am studying Statics and saw that:

The moment of a force about a given axis (or Torque) is defined by the equation:

$M_X = (\vec r \times \vec F) \cdot \vec x \ \ \ $ (or $\ \tau_x = (\vec r \times \vec F) \cdot \vec x \ $)

But in my Physics class I saw:

$\vec M = \vec r \times \vec F \ \ \ $ (or $\ \vec \tau = \vec r \times \vec F \ $)

In the first formula, the torque is a triple product vector, that is, a scalar quantity. But in the second, it is a vector. So, torque (or moment of a force) is a scalar or a vector?

Qmechanic
  • 220,844
Vinicius ACP
  • 798

3 Answers3

3

Torque (Force Moment) is a vector that describes the location of the Force line of action.

  • Lemma: If you give me a force vector ${\vec F}$ and a moment vector about the origin ${\vec M}$ then I can define a line whose points obey the relationship $\vec{M} = {\vec r} \times {\vec F}$. This line has direction parallel to the force ${\vec F}$ and passes through a point (closest to the origin) defined by $${\vec r} = \frac{ {\vec F} \times {\vec M} }{ \| {\vec F} \|^2 } $$

Proof: Use $\vec{M} = {\vec r} \times {\vec F}$ into the equation for the point.

$$ \require{cancel} \frac{ {\vec F} \times {\vec M} }{ \| {\vec F} \|^2 } = \frac{ {\vec F} \times ({\vec r} \times {\vec F}) }{ \| {\vec F} \|^2 } = \frac{ \vec{r} ( \vec{F} \cdot \vec{F}) - \vec{F} (\cancel{\vec{F} \cdot \vec{r}} ) }{ \| {\vec F} \|^2 } = \vec{r} \frac{\| {\vec F} \|^2}{\| {\vec F} \|^2} = \vec{r} $$

This requires that $\vec{F} \cdot \vec{r}=0$ which is true for the point on the line closest to the origin.

It is true for both statics and dynamics that a moment is just a force at a distance. Only when the net force is zero (force couple) the moment is a pure moment and it does not convey any location information.

John Alexiou
  • 40,139
2

There are some application, where we might want to quantify both the torque, which is a vector, and the component of the torque about a particular axis, which is a scalar.

I illustrate an example of this in the figure below, which is from 1 and provided here under fair use for the purpose of scholarship. The door is hinged so that it turns only around the $\mathbf{\widehat{k}}$ axis. Meanwhile, the door knob is located at a position $\mathbf{r}$ relative to the origin. A force $\mathbf{F}$ is applied to the door knob.

By $\boldsymbol{\tau}$, I denote the torque on the door knob, which is $$\boldsymbol{\tau} = \mathbf{r}\times \mathbf{F}.$$ By $\tau_z$, I denote the scalar component of the torque vector about the axis of rotation. So, $$\tau_z = \mathbf{\widehat{k}} \cdot \boldsymbol{\tau} = \left(\mathbf{r}\times \mathbf{F}\right)\cdot \mathbf{\widehat{k}}.$$

enter image description here

Bibliography

1 Mathematical Methods in the Physical Sciences, 3rd Edition, Mary L. Boas, ISBN: 978-0-471-19826-0 July 2005.

Michael Levy
  • 775
  • 6
  • 15
1

It is obviously a vector, as you can see in the 2nd formula.

What you are doing in the first one is getting the $x$-component of that vector. Rememebr that the scalar product is the projection of one vector over the other one's direction. Actually you should write $\hat{x}$ or $\vec{i}$ or $\hat{i}$ to denote that it is a unit vector. That's because a unit vector satisfies

$\vec{v}\cdot\hat{u}=|v| \cdot |1|\cdot \cos(\alpha)=v \cos(\alpha)$

and so it is the projection of the vector itself.

In conclusion, the moment is a vector, and the first formula is only catching one of its components, as noted by the subindex.

FGSUZ
  • 8,573