Is it always possible to define energy of a system?

Question

Does the concept of energy always exist for any physical system? If yes is there a proof? If no, any counterexamples?

Answer 1

Gravitational energy in GR is a notoriously tricky concept to define, see e.g. the Wikipedia page on stress-energy-momentum (SEM) pseudotensor; or this, this & this Phys.SE posts and links therein.

Answer 2

The usual practice is to define an arbitrary state of the system as an energy of zero. For example if I have a 100g wooden ball in a room, I might choose to define the zero state as when the ball is resting on the floor.

If the ball is moving around or in an elevated position the energy of the system (with respect to the reference state) would be positive with respect to my reference state.

On the other hand if I were to burn the ball and allow the thermal energy to escape from the room, the energy of the system would now be negative with respect to my reference state.

In other words if someone asks "how much energy does this system have" the answer is "with respect to what alternative state?"

There are many conventions, which may be convenient for different situations. For example if the system consists of one electron and one proton, different individuals might define zero energy as:

1. with the electron at infinite distance from the proton
2. with the electron at the limit of being captured by the proton to form a hydrogen atom
3. with the electron and proton as a hydrogen atom, in its ground state.

In general the amount of energy required to bring about a defined change in state is very well defined.

On the other hand The concept of how much energy a system contains is meaningless, unless an appropriate reference state for the system has been defined.

Everyone would agree that the energy difference between states 2 and 3 in the above example is a certain value (known as the "ionization energy" of the hydrogen atom) which can be found in tables. Note that the "ionizaton energy" is in fact an energy difference, or, alternatively, the amount of energy needed to change between two well defined states.

Confusion could arise when people from different disciplines meet and have different ideas about what the reference state for "zero energy" is for a system. For the 1 proton, 1 electron system, all three of the above are in use.

There is one little trick you can employ if you really want to have an absolute definition of the energy content of a system. That is, to define its energy in terms of its mass, in accordance with Einstein's equation E=mc^2. The numbers obtained, however, are so vast that energy comparisons of everyday mechanical and chemical changes of state become impractical.

As an analogy, consider that architects measure height from ground level and cartographers measure height from sea level, but nobody measures height in the most fundamental way, namely distance from the centre of the earth.

Answer 3

In theory of course it is possible to imagine systems that have no defined energy.

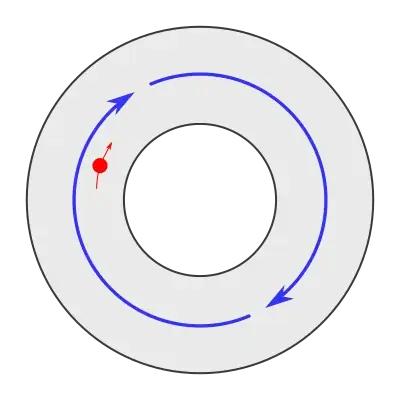
Imagine a universe shaped like a disk with a hole in it. A force-field goes around it in a circle, and a single particle spinning around at an ever-increasing rate:

Now try to think how you would define an energy in terms of the particle's position and velocity that would control how the particle moves.

Of course, whether such a system could exist in the real world, I have no idea.