Why and how Dirac cones are "tilted"?

Question

Given a Weyl Hamiltonian, at rest,

$$ H = \vec \sigma \cdot \vec{p} ,$$

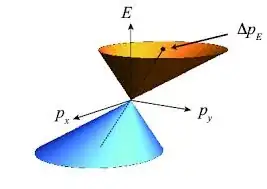
A Lorentz boost in the $x$ direction returns $ H = \vec\sigma\cdot\vec {p} - \gamma\sigma_0 p_x$.

The second term gives rise to a tilt in the "light" cone of graphene. My doubts are:

How I can derive such term given a Lorentz transformations in x direction? If the cone of "light" is "tilted" then the Fermi velocity has changed?

Reference: Tilted anisotropic Dirac cones in quinoid-type graphene and α−(BEDT-TTF)2I3. M.O. Goerbig et al. Phys. Rev. B 78, 045415 (2008), arXiv:0803.0912.

Answer 1

The Dirac cone in solids is emergent. Since the Dirac theory in solids is mounted on a lattice, depending on the connectivity of lattice (hopping pattern) and geometry of the lattice (some non-symmorphic lattices), the tilt can be introduced. In certain two-dimensional lattices, the perpendicular electric field (displacement field) can couple to the tilt and tune it. So in principle the tilt can be controlled (see Ref. 1 below).

Moreover, once the tilt is there, it can be neatly described by a metric. This metric will be a deformation of Minkowski metric which has interesting consequences for solids. For more details, please see:

1. Electric field assisted amplification of magnetic fields in tilted Dirac cone systems. S.A. Jafari, Phys. Rev. B 100, 045144 (2019), arXiv:1904.01328.
2. Polarization tensor for tilted Dirac fermion materials: Covariance in deformed Minkowski spacetime. Z. Jalali-Mola and S.A. Jafari, Phys. Rev. B 100, 075113 (2019), arXiv:1904.13277.
3. Electrodynamics of tilted Dirac/Weyl materials: A unique platform for unusual surface plasmon polaritons. Z. Jalali-Mola, S.A. Jafari, arXiv:1908.07082 (2019).