You're right, the charge build-up won't be uniform over the hemisphere.
This is a rather standard example of using the method of images where space is separated into two regions by a conducting surface (inside and outside a sphere or above and below an infinite plane are some classic examples).
You may then replace the net effect of the charge distribution on the (grounded or uncharged) conducting surface with an equivalent "image charge" which satisfies the same boundary conditions (usually the value of the potential on the conductor), and solve that problem which is generally considerably simpler. The uniqueness theorem in Electrostatics then implies that the solutions to both these problems should be the same, as they both satisfy the same boundary conditions.
I could write out a solution, but there's already one given on the Wikipedia page, as well as a rather good one here, which seems quite detailed.
There is a very good answer to a similar question that could also help you.
EDIT: I'm including a hint at the solution for an ungrounded sphere.
Finding the potential:
The method of images works well when we assume a grounded sphere (so that the potential $V=0$ on the surface). However, with a small modification, the same basic model can also handle a sphere at an arbitrary potential $V_0$. We do this by introducing a second charge.
As shown on this page, the solution for the potential of a grounded sphere of radius $R$ and a charge $+q$ at a distance $z=a$ ($a>R$) from its center is given by replacing the entire sphere with an induced charge $$q' = -\frac{q R}{a}$$
at a position $$z = \frac{R}{a^2} < R$$
As I explained, both these problems are guaranteed to have the same solution by the uniqueness theorem. How do we extend this to a sphere at some arbitrary potential? We need to increase the potential on the surface of the sphere while keeping it an equipotential surface! It should be quite obvious that the way to do this is in fact to introduce a second image charge (say $q''$) at the center of the sphere $z=0$. Since potentials are additive, this merely changes the potential on the surface of the sphere from being $V=0$ to a constant $V = V_0 = \frac{1}{4\pi \epsilon_0}\frac{q''}{R}$, where $q''$ can be chosen depending on $V_0$.
If the sphere is neutral (as is the case in your problem) then we simply require that $q' + q'' = 0$. Thus, you would now need to find the potential for the following problem 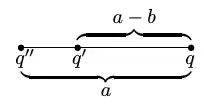
which is a trivial extension that you should be able to do if you've understood how to do the grounded case, but with 3 terms this time, the third being the potential due to the charge $q'' = -q'$ at the origin.
Finding the surface charge density:
The field within a conductor is zero, and the field outside infinitesimally close to it is given by
$$\mathbf{E} = -\mathbf{\vec{\nabla}}V = \frac{\sigma}{\epsilon_0}\mathbf{\hat{n}}$$
(If you're having trouble with this part, I would very strongly advise you to read Chapter 2 in Griffith's Electrodynamics. I haven't seen it better explained anywhere else.)
Thus if we know the potential $V$ using this formula, we can calculate the surface charge density. Defining
$$\frac{\partial V}{\partial n} = \vec{\nabla}V \cdot \mathbf{\hat{n}}, \quad \quad \quad \quad \implies \sigma = -\epsilon_0 \frac{\partial V}{\partial n}\Big|_\text{on the surface}$$
So, the case of the sphere is pretty simple, since on the surface of the sphere the normal direction is $r$. Once you've found $V(r,\theta)$, you can easily find
$$\sigma(\theta) = -\epsilon_0 \frac{\partial V(r,\theta)}{\partial r}\Big|_{r=R}$$
which you should be able to do. If you'd like to check your results, here are two solutions:
1) For a grounded sphere, the induced surface charge density is given by
$$\sigma_0 (\theta) = \frac{q}{4\pi R}\left( R^2 - a^2 \right) \left(R^2 + a^2 - 2 R a \cos\theta \right)^{-3/2}$$
(You could check this by integrating over all $\theta$. What should the result be?)
2) For an ungrounded sphere,
$$\sigma(\theta) = \sigma_0 (\theta) + \frac{q}{4 \pi R a}$$
