0

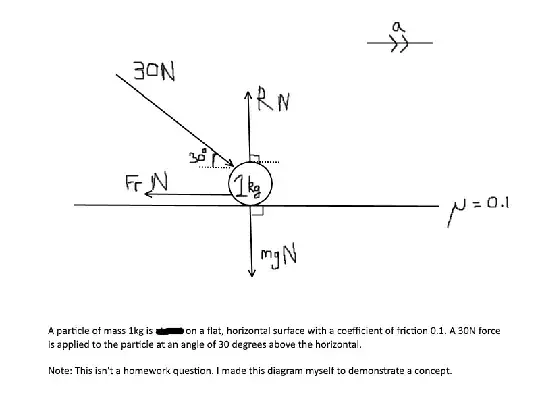
enter image description here

$R$ = Normal reaction force exerted on the particle by the ground

$Fr$ = Frictional contact force between the particle and the ground

All forces are measured in Newtons ($N$)

Using the angles we can calculate the forces acting on the particle.

$$m=1, \ \ \ mg = g = 9.8N$$

Netwton's Third Law of motion states that if A exerts a force magnitude N on B, then B exerts a force of maginitude N on A, but in the opposite direction. Hence:

$$R = 9.8 + 30 \ sin(30)$$ $$R = 24.8N$$

Now, if we also go by Newton's Third Law, then if the particle is pushing forwards on the ground with a force magnitude N, then the ground is pushing backwards on the particle with a force magnitude N, which should be friction. However:

$$30 \ cos(30) = 26.0N$$ $$Fr_{(max)} = R \mu = 2.48N$$ $$Fr_{(max)} < 26.0$$

Due to the limit on friction set by the coefficient of friction between the surface and the particle, the particle accelerates with acceleration $a$. However, this appears to contradict Newton's Third Law, which clearly states that $Fr$ should equal $30 \ cos(30)$.

This is especially strange since $R$ follows Newton's Third Law perfectly without a limit, so why does friction appear to disobey it?

What am I missing here?

Pancake_Senpai
  • 1,367

2 Answers2

2

One word on notation: in general, you should put units everywhere, and not just now and then. An equation like $30 \cos(30)=26.0N$ is unacceptable; either state that you're going to measure all forces in $N$ and don't bother writing the $N$, or write it everytime.

Okay, so onwards to the answer. First, your calculation of the normal force is correct but it's not because of Newton's third law, it's because of the second. You simply set the sum of vertical components equal to zero.

The problem in your reasoning is that the force that the object exerts on the ground is not the horizontal component of the pushing force. The only possible horizontal force between the object and the ground is friction, so the action-reaction pair is just the two friction forces the object and the ground exert on each other. According to your calculations, the frictional force turns out to be $2.48\, \mathrm{N}$ (actually we would need the dynamic coefficient but let's keep it simple). Therefore, your object exerts a force on the ground with horizontal component equal to $2.48\, \mathrm{N}$ in the forward direction.

How you can you tell that the $30\, \mathrm{N}$ force is unrelated to the ground? Well, look at your diagram. That force is being exerted by your hand (presumably) and it acts on the object, so that is the pair you care about. If you want to apply Newton's third law to the object-ground system, look at the picture again: the forces being exerted by the ground are the normal force and friction. Those are the ones you care about.

Javier
  • 28,811
2

First of all, you don't need to write $_{max}$ or talk about limits when it is kinetic friction. Kinetic friction has a fixed formula. That formula is:

$$F_r=\mu N$$

and not $F_r=\mu R$. Don't use the reaction force $R$, only the normal force $N$.

Now, this friction is what the ball affects the surface with. It is not the reaction force, which affects the surface, it is the friction which does.

The ball affects the surface with friction, and the surface holds back with the same force in the ball, yes. This is Newton's 3rd law.

this appears to contradict Newton's Third Law, which clearly states that $F_r$ should equal $30 \cos(30)$.

This is not correct, as I stated just above. The $30 \cos(30)$ is the reaction force's horizontal component $R_x$, but that is not the force that affects the surface. This $R_x$ causes friction, you could say, but they are not equal - Newton's 2nd law says that:

$$R_x-F_r=ma\quad\Leftrightarrow\quad F_r=R_x-ma$$

The $R_x$ is clearly larger than the friction $F_r$; the rest of $R_x$ Is used for acceleration.

Bill N
  • 15,522
Steeven
  • 53,191