1

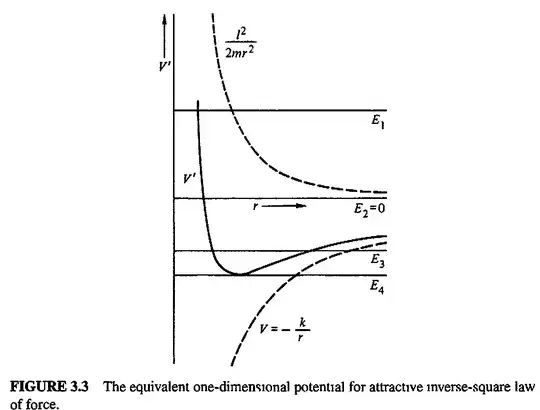
The relevant figure is below (taken from Goldstein's Classical Mechanics). This figure plots the effective potential for a gravitational force. Does the effective potential $V'$ go flat below $E_2=0$? After finding $r_{flat}$, the point where the effective force $f'=0$ (or equivalently, where $V'$ goes flat), I got $$V'(r_{flat})=-\frac{mk^2}{2l^2}$$ Now, it looks like this is expression is negative since $m$,$k$, and $l$ are all positive. So my question is: Doesn't this result in a possible parabola that could have an energy less than $E_2=0$? I know it isn't possible for a parabola to have negative energy, so where am I going wrong in my reasoning?

Thanks.. enter image description here

Joebevo
  • 2,291

2 Answers2

2

I) The fictitious potential

$$\tag{1} V^{\prime}~=~V+\frac{\ell^2}{2mr^2} $$

is a sum of a Newtonian gravitational potential

$$\tag{2} V~=~-\frac{k}{r}, $$

and a centrifugal potential. The mechanical energy is a constant of motion and given by

$$\tag{3} E~=~\frac{1}{2}m\dot{r}^2+V^{\prime}. $$

See also this Phys.SE question.

II) OP correctly calculates that the minimum point is

$$\tag{4} r_0~=~\frac{\ell^2}{mk},$$

and that the minimum value is

$$\tag{5} E_4~:=~V^{\prime}(r_0)~=~-\frac{mk^2}{2\ell^2}.$$

III) Despite what the Figure 3.3 may suggest, there is no gap between the limit $\lim_{r\to\infty} V^{\prime}(r)$ and $E_2:=0$. The potential $V^{\prime}$ is a monotonically growing function in the whole interval $r\in[r_0,\infty[$, with the limit

$$\tag{6} \lim_{r\to\infty} V^{\prime}(r)~=~0, $$

as can be easily deduced from the first two formulas (1) and (2). The energy $E=E_2:=0$ corresponds to a parabolic orbit, while the energy $E<E_2:=0$ corresponds to an elliptic orbit.

Community
  • 1
Qmechanic
  • 220,844
0

The effective potential energy is not the same as the orbital energy. The orbital energy is a constant of the orbit, while the effective potential energy varies throughout the orbit. For a parabolic orbit the orbital energy is always zero, but the effective potential energy varies between positive and negative depending on the phase of the orbit.

The effective force is zero when the effective potential equals $E_4$. $E_4$ is always negative regardless of the eccentricity of the orbit.

Nick
  • 1,642