2

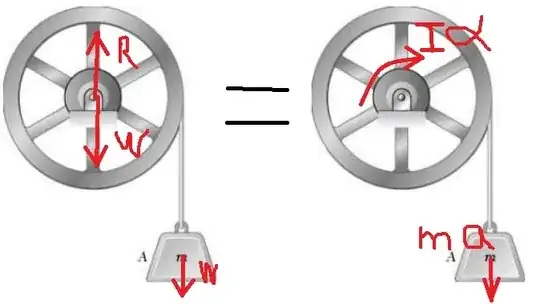
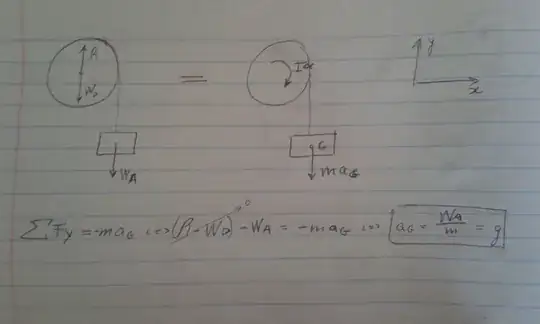
Does Alembert work for systems of rigid bodies? My question comes from this image. (sorry for the poor drawing!)

Drawing

I'm trying to find the acceleration of the block exclusively from the sum of forces in the y component, but when I do so I get $a=g$, which is the same as an object in free fall. On the other hand, if I use the relationship between angular acceleration and linear acceleration I find the right answer. Why can I not sum the forces in the $y$ direction and take $a$, that is the only question.

Here are the calculations: e

Qmechanic
  • 220,844
George Sailor
  • 79

2 Answers2

2

This is how you can solve this problem using Lagriangian mechanics, which has D'Alemberts principle built in.

Call the height of $m$ $q$. The Langrangian becomes:

$$\mathcal{L} = T-V = \frac{1}{2}m\dot{q}^2+\frac{1}{2}I\left(\frac{\dot{q}}{R}\right)^2 - qgm$$

Therefor: $$\frac{d}{dt}\left(\frac{\partial \mathcal{L}}{\partial \dot{q}}\right) = \frac{\partial \mathcal{L}}{\partial q} \implies m\ddot{q} + \frac{I}{R^2}\ddot{q}=-gm$$

Now solve for $\ddot{q}$: $$\ddot{q}=\frac{-gm}{m+\frac{I}{R^2}}$$

QuirkyTurtle98
  • 449
0

You first need to construct the free body diagrams of hanging mass and rotating disc.

For the mass there are two acting forces : tension force of the rope $T$ and gravitational force $m g$. So its equation of motion will be : $m g - T = m a$

For the disc, you have reaction of the tension force on tangential axis and constraint force on the pin joint. So disc is translationally static. However, tangential force makes disc rotate which can be captured by the differential equation $T R = I \alpha$.

By kinematics, we have $\alpha = a/R$ which leads to $T = I a /R^2 $. Substituting this relation of tension force $T$ in equation for mass, you obtain $m g = a (m + I/R^2)$. Thus, $a = (m g) / (m + I/R^2)$ simply.

Gorkem Secer
  • 11