Can an object be perfectly flat?

Question

I ask myself this question from a microscopic point. I assume that at our scale it's pretty easy to say that an object is flat or not.

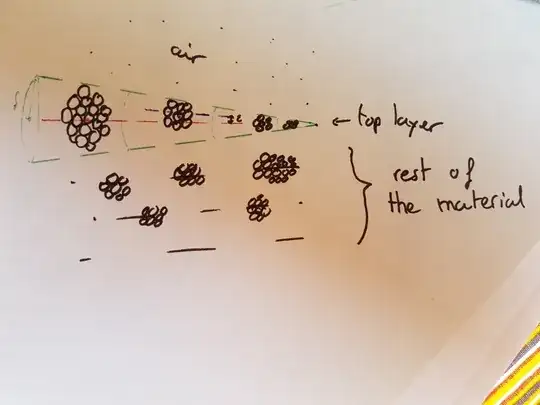
You need to imagine that we are at the top layer of a material. Above there is air and below the tube there is the rest of the material. The tube is just the top layer of the material with radius $\delta$, considered as the radius of a nucleus !

My question is : If we define this material as flat, does it mean that the top layer is perfectly aligned (Fig 1) or can we consider some little error $\varepsilon > 0$ (Fig 2) ? $\varepsilon$ is defined as the difference between the center of 2 nucleus

Answer 1

A perfect "flat" surface does not exist and taking q.m. into account is not a meaningful concept. As pointed out by the others, even the radius of an atom is not uniquely defined (e.g. $1/e$ radius, ...).

A pragmatic approach is as follows:

• First step: Define roughness. Instead of "flatness" people prefer the concept of "roughness", which is the deviation of "flatness". As always, there exists different definitions of roughness, e.g. \begin{align} \textrm{"absolute" roughness value: } R_a &= \sum_j |r_j - \mu| = \sum_j |\delta_j|\\ \textrm{"RMS" roughness value: } R_q &= \sum_j (r_j - \mu)^2 = \sum_j \delta_j^2\\ \end{align} where $\mu = \sum_j r_j$ is the mean value -- instead of sums we should use integrals if $r$ is a continuous variable.
• Second step: Splitting into wavelength. As you pointed out in your question, it is not meaningful to speak about flatness in general. Therefore, we speak of roughness in specific wavelength (or spatial frequency) bands. E.g. it makes perfect sense to speak about a RMS roughness of 1nm in the wavelength band [$1\mu m$ ... $50\mu m$].
• If you are interested in material properties and which materials can be best polished, I recommend you read how the unit "kilogram" is defined and how it could be defined.