2

I have a doubt about the derivation of the Kutta-Joukowski theorem for a Joukowski airfoil. I know the results, but my main objective is to know how get these ones.

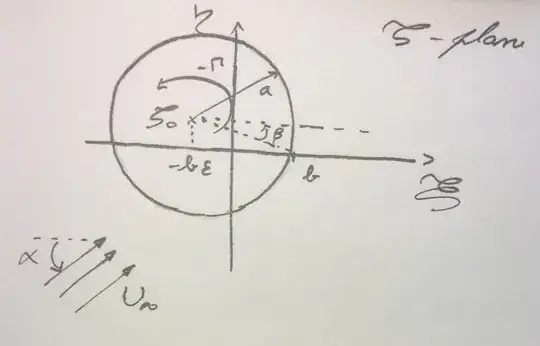
Consider for the initial plane a cylinder centered on $\zeta_0$, with a circulation -$\Gamma$, in an uniform flow with an atack angle $\alpha$:

where $a$ is the circumference radius, and $b$ the intersection of the circumference with the real positive axis, $\xi$. The parameter $\beta$ is the angle between the horizontal line and the line that links $\zeta_0$ to $b$. The center of the circumference is:

$$\zeta_0=b-ae^{-i\beta}$$

enter image description here

For this flow we have the following complex potential:

$$W(\zeta)=U_\infty\left[e^{-i\alpha}\left(\zeta-\zeta_0\right)+\frac{e^{i\alpha}a^2}{\left(\zeta-\zeta_0\right)}\right]+\frac{i\Gamma}{2\pi}\ln\left(\zeta-\zeta_0\right)$$

The Joukowski transform is:

$$z=\zeta+\frac{b^2}{\zeta}$$

To determine the complex potential on the $z$ plane we need to find the relation between $\zeta$ and $z$. And we get:

$$\zeta=\frac{z}{2}\pm\sqrt{\left(\frac{z}{2}\right)^2-b^2}$$

That is an awful relation. We not only have a square root, but also an $\pm$ symbol. Substituting this on the potential complex and then find the residues of $\left(\frac{dW}{dz}\right)^2$ and $\left(\frac{dW}{dz}\right)^2 z$ would be pratically impossible. What should be the next steps?

[Note: I didn't find any paper or book that shows the derivation of this theorem on the $z$ plane, but only on the $\zeta$ plane, which I already know. Do you know anything that can help me?]

Élio Pereira
  • 1,102

1 Answers1

1

you have transformed circle into ellipse by, $z = \zeta + \frac{b^2}{\zeta}$ ,

Now you have to do the inverse by tranforming ellipse into circle,

So the standard text books (Milne Thompson, etc) use,

$\zeta = \frac{1}{2}z + \frac{1}{2}{\sqrt{z^2-4b^2 }}$ .

Myself tried to transform ellipse into circle with the aove and suceeded.

mustang
  • 133