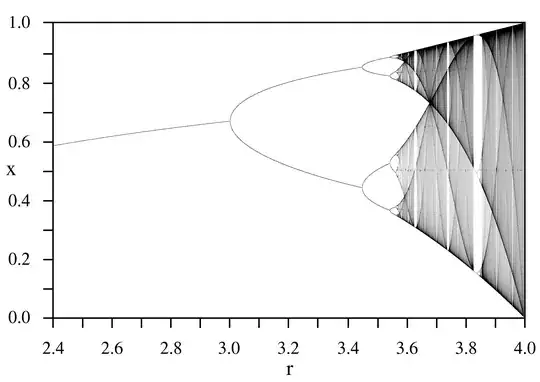
The stadium billiard is known to be a chaotic system. This means that the only integral of motion (quantity which is conserved along any trajectory of motion) is the energy $E=(p_x^2+p_y^2)/2m$.
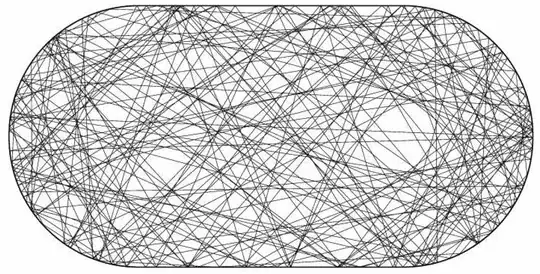
Why are we sure that no other, independent on $E$, integrals of motion exist in this system? One can assume existence of some, perhaps infinitely complicated, function $I(x,y,p_x,p_y)$, which is conserved and independent on $p_x^2+p_y^2$. Why is this assumption wrong?
In other words: the simplest prototypical examples of integrable billiards (rectangular, circular, elliptical) have some obvious symmetries allowing us to find two independent integrals of motion. What if, in some other billiard, such integrals do also exist, but are not so obvious and have no simple analytical form? How can we distinguish two situations:
there exist two independent integrals of motion, so the system is integrable, but their form is very complicated,
the only integral of motion is $E$ and other independent integrals are absent?
I'm not a specialist in dynamical systems and related complicated mathematics, so any simple explanations will be appreciated. I've found the related questions Idea of integrable systems and Non-integrability of the 2D double pendulum but didn't get any simple answer.