How do Black Hole event horizons grow?

Question

I was trying to understand how matter falls into black holes, and I got confused by this thought experiment.

1. A small mass falls into a black hole (which negligibly effects the Schwarzschild radius)
2. A sufficiently long time later (as measured by a distant observer) a large mass falls into the black hole
3. The event horizon expands to engulf the smaller mass?

I realize this kind of reasoning is prone to misconceptions about simultaneity and the like, but I don't know how to think about it more rigorously. I also know that $g_{rr} \rightarrow \infty$ as $r \rightarrow r_s$ in the Schwarzschild metric.

In short: How does the event horizon grow when mass is added?

Answer 1

Yes they grow as mass or energy is added in. It's not complicated, and well understood, within General Relativity. With one caveat.

The caveat if that a body that almost reaches the horizon gets so close to it even as time slows down infinitely (theoretically) that for all practical purposes you can cconsider it to have been absorbed into the black hole (BH). That deals with the confusing issue of time slows infinitely at the horizon. It's dealt with in other questions on this site

The horizon radius of a Schwarzschild BH is (first reference at bottom)

$R_h = 2GM/c^2$

There's an equation for rotating and charged BHs also, with the the charge and angular momentum entering in. The details are not too important for the purposes here.

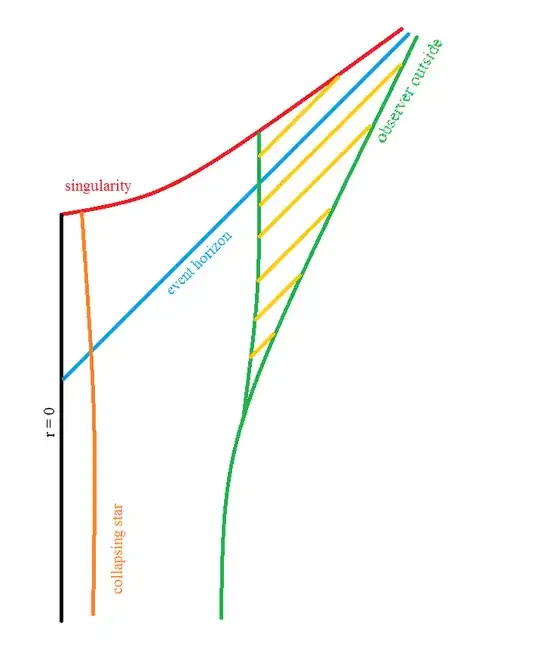
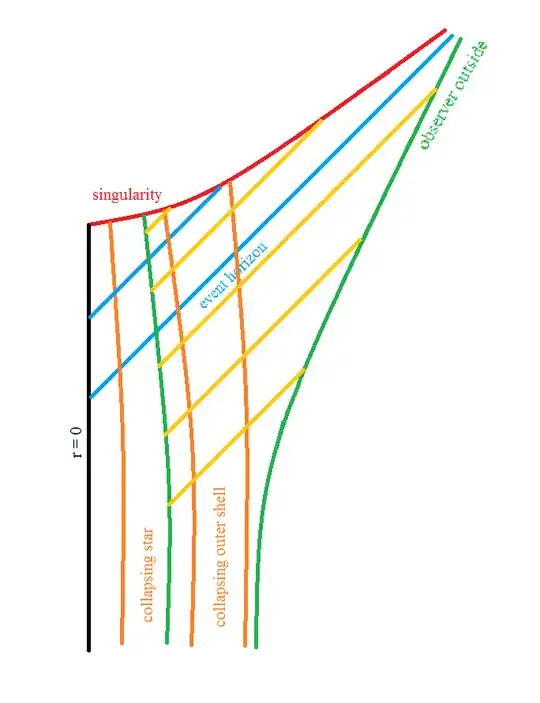
When matter is added, carefully and radially to make sure it does not add angular momentum, the horizon radius increases proportionately to the amount of mass added (but see below you may also be adding 'kinetic and potential energy' in, so it must be accounted as part of the toal mass, or energy, added). Simple from the equation, thehorizon grows. In realistic simulations with small masses added in the exact calculations show the horizon reaching out some to meet the added mass and swallow it. A similar effect is true for rotating black holes. Except for Hawking radiation which is a quantum effect, nothing escapes the BH and the radius can grow or stay the same (if no matter added), but never decrease. The surface area of the horizon increases as the square of the radius.

If you add a larger mass it increases that much more. If the mass being added is from an extended body, the gravity of the BH can be enough to break up that body with tidal forces and have parts of it flowing into the BH first, until it swallows it all up. If the body was orbiting around the BH, it'll fall in partially in tangential orbits, and add angular momentum to the BH (and then we have to use the Kerr metric).

Note that these property of the BH horizons 'rising' to meet the incoming mass, i.e., the distortion of the horizon as an external disturbance affects it, can also be seen for instance in this simulated video of two BHs merging at https://m.youtube.com/watch?v=I_88S8DWbcU. Notice the distortions of the horizons as they come closer. Others simulations have shown the effect also.

In general the equations for BH thermodynamics, which describes how BHs can grow, , i.e. how it's parameters can change, is given from the second reference below, as

dE = (k/8$\pi$) dA + $\Lambda$ dJ + $\Phi$ dQ

where the E is energy (mass), the second term is term is angular velocity times change in angular momentum (i.e., rotational energy), and the third is the electrical energy as electrical potential time the charge change in the BH (eg, by accretion of charge). The second law of BH thermodynamics is that

dA can not be negative (since A is proportional to entropy which cannot decrease).

Thus, not only can they accrete matter, but also charge and angular momentum. It turns out that one can also extract angular momentum and charge from the BH, and thus energy. Just the amount of energy/mass corresponding to the area A can not be made lower, since A cannot decrease. It's sometimes called the irreducible mass.

https://en.m.wikipedia.org/wiki/Schwarzschild_radius https://en.m.wikipedia.org/wiki/Black_hole_thermodynamics

Answer 2

It's essentially right, but I think better to consider matter being apparently stopping at the event horizon due to the effects of time dilation - to call that "falling into" can be a bit misleading. As you suggest further matter can effectively bury it by increasing the Swarzchchild radius.

Answer 3

To understand black holes properly you should go beyond the Schwarzschild coordinates view. They are good when you sit outside black hole but not very useful to properly understand what happens at horizon. They behave badly there but this is purely coordinate effect. It's even problematic to say that "for outer observer the infalling object never falls in". All you can say objectively is that some local interactions happen such as that "for outer observer the infalling object never seem to fall in" i.e. he/she never recieves the corresponding signals from the infalling object. My favourite example how naive thinking can break your head is de Sitter spacetime that's simultaneously is closed, flat and open expanding universe.

To understand what happens properly you should take other coordinates that show causal structure of the spacetime. For spherically symmetric case, \begin{equation} ds^2=A(t,r)dt^2+2B(t,r)dt\,dr-C(t,r) dr^2-r^2d\Omega^2 \end{equation} you can concentrate on $(t,r)$ sector where you can find coordinates $(u,v)$ in which metric takes the form, \begin{equation} ds^2=f(u,v)\Big(du^2-dv^2\Big)+r(u,v)^2d\Omega^2 \end{equation} then all lightlike signals moving in $(t,r)$ plane will lie on $u+v=0$ or $u-v=0$ forming cone like in 2d Minkowski spacetime. All timelike curves and lightlike signals moving somewhat at angle to radial direction will lie inside that cone.

For collapsing black hole that gives the following picture. Remember lightlike signals are at $45^\circ$,

So you can see two important differences from the usual logic. First the singularity inside the black hole is not a point in space - it's a moment in time, "the end of days" for the interior. Second the horizon is simply some light cone. Going inside any light cone inside any spacetime without closed timelike curves nothing slower than light can leave it anymore. The difference from the usual lightcone in the flat Minkowski spacetime is that outside the black hole the spacetime is curved in such a way that it admits Schwarzschild-like description of it being surface of asymptotically constant radius.

The observer to stay outside has to constantly accelerate and in terms of $(u,v)$ traces hyperbola-like wordline that may approach the horizon asymptotically but never crosses it. So let's imagine that the observer throws inside the probe that constantly sends radioreports back. What happens is that the closer to the horizon the signals are sent the later they cross the hyperbolic wordline of the observer. To recieve the signals from just over the horizon the observer will have to wait very long. That's how you get that the observer never sees the infalling object crossing the horizon.

If you drop something large so that you can't smoothly connect the horizons it's basically so that would be if the larger black hole forms from the collapsing matter that includes smaller black hole. E.g. you can envision the collapsing matter surrounded by some dust cloud that itself collapses. In that case we can mostly schematically use the following picture,

where we have inner horizon and larger and in terms of $u$ earlier horizon of the resulting larger black hole. What happens with experiment with probe then? We see that signals from the probe below the new horizon but above the inner horizon don't reach the observer at all!

So no signal about what happens just above the smaller black hole horizon manages to reach outside the larger black hole

Answer 4

I am answering this in the hope that somebody will tell me if I am wrong.

I would ask you to forget the event horizon for a moment.

We know nothing about what goes on inside the event horizon, so what exactly happens the black hole mass (in a physical sense) is based, to a small extent, on extrapolations of what we do know happens neutron stars, as with these we can indirectly observe the physical effects of very high orders of mass density.

It seems likely that once a black hole forms, no matter how much mass you put into it, a singularity is formed. I could speculate on the "size" of the singularity, i.e. does it get bigger as we put more mass in, but the distortion of space time caused by the singularity may make any ideas of size or dimensions as we understand them, (very) probably not physically visualizable to 3 dimensional humans.

So all we are left with is the knowledge of only the mass, (and therefore the gravitional effect associated with this mass), the electric charge and the spin of the black hole.

The surface area of the event horizon is directly linked to the mass inside, but what happens that mass is unknown, other than a seemingly reasonable conclusion that it reaches densities greater than anywhere else in the universe. I am not sure that anybody can tell you what that infinite density then produces or results in.

On one level, the notion of how the increased mass increases the size of the event horizon is no different than if we doubled the Earth's mass and thereby produced increased gravity in line with Newton's law of gravitation.

But in the case of a black hole, when this mass may be transformed into "whatever" (the singularity), how it manages to increase the size of the event horizon is still hypothetical.