Gravitation is not force?

Question

Einstein said that gravity can be looked at as curvature in space- time and not as a force that is acting between bodies. (Actually what Einstein said was that gravity was curvature in space-time and not a force, but the question what gravity really is, is a philosophic question, not a physical one)

Answer 1

Websters specifically defines force as the gravitational interaction (definition 4b). We all were taught in high school that gravity was a force.

Given the lack of consensus among the authorities, a more edifying, less controversial, and equally true statement might be:

In general relativity, gravity is a fictitious force.

In classical mechanics, fictitious forces are not considered "real" forces. However, nobody, not even relativists, goes around claiming "the Coriolis force is not a force".

The issue of gravity being a force or not has nothing to do with general relativity. If you believe that inertial forces are forces, then gravity is a force. If you believe that inertial forces are not forces, then gravity is not a force.

Answer 2

In GR, there are always two points of view--- local and global. In the local point of view, you look in a neighborhood of a point, and make a free-falling frame, and then motion is entirely in straight lines at constant velocity so that you don't see gravity. In this way of looking at it, gravity is not a "force", meaning it doesn't make a generally covariant contribution to the local curvature of the particle space-time paths.

In the global point of view, you see an incoming particle from infinity deflected by a field, and you say a force has been acting if the particle is deflected. In this point of view, every deflection is a force by definition.

The global point of view is the way in which gravity is treated in quantum field theory or string theory. The local point of view is the insight due to Einstein, and it is no surprise he would emphasize it in his public remarks.

The answer is "it depends on your philosophical definition of force, whether you take a local view or a global view." I prefer the global view, since it is more quantum, so I say gravity is a force, but I don't disagree with people who take the other view, since it is also valuable.

Answer 3

Well, if we're talking about what Einstein said, then the way Einstein defined gravitational field and gravitational force in GTR is that it is given by the connection, with its components by the Christoffel symbols: $$\Gamma^{\alpha}_{\mu\nu} = \frac{1}{2}g^{\alpha\beta}\left[g_{\mu\beta,\alpha}+g_{\nu\alpha,\beta}-g_{\mu\nu,\beta}\right]$$ where commas denote partial derivatives and the metric $g_{\mu\nu}$ plays the role of gravitational potential.

But this is quite different from Newtonian gravitational force.

In Newtonian mechanics, you have 'real' forces and 'inertial' (aka "fictitious") forces, the difference being that you can make inertial forces disappear by adopting an inertial frame. For example, Newton's laws in a uniformly rotating reference frames introduce centrifugal and Coriolis forces that are proportional to the mass of the object acted upon and can be removed changing to an inertial, and hence non-rotating, frame.

In other words, inertial forces are the "fault" of choosing a non-inertial frame of reference.

By the above definition, gravity is an inertial force. Similarly to the Newtonian case, it can be made to disappear by changing the reference frame--but there is also a big difference: in the Newtonian framework, inertial frames are global, and so inertial forces disappear everywhere. In GTR, that's no longer the case: there are only local inertial frames in general, and so you can only make it disappear locally.

Caution: modern treatments of general relativity do not adopt this definition. Many of them (e.g., Misner, Thorne, and Wheeler) intentionally do not identify either 'gravity' or 'gravitational field' with any particular mathematical object, not the connection, not the curvature, nor anything else. But then (for MTW) it is not technically correct to say that gravity is spacetime curvature either, but rather refers "in a vague, collective sort of way" to all of these geometrical constructs.

Answer 4

Gravity is not a force. It looks like a force because objects with non-zero rest mass have always a non-zero time-like component to their 4-velocity tangent vector to their worldline in the spacetime manifold. In other words, no mater how fast or slow you move relative to anything through space, your time coordinate may look smaller or bigger with respect to those things, but never zero. As long as you have mass, you cannot stop the flow of time for you, not even by accelerating, in flat or even curved spacetime.

Since you cannot stop in time, if spacetime is curved by a massive object like Earth, your motion through curved time will keep bumping you against it. The real force is the electromagnetic attraction between the Earth's crust particles (and the seat of your chair, ground of your house, etc!) preventing you from going all the way to the center of the Earth.

Good books that helped me really understand this (and the wonderful diagram in answer Jul 18 '13 at 12:31 by user Calmarius) are The Large Scale Structure of Spacetime by Stephen Hawking, Gravitation by Misner, Thorne and Wheeler, Spacetime and Geometry by Carrol, Introduction to Smooth Manifolds by Lee, among several others, plus sitting in topology and differential manifolds courses at my local university.

Heck, just look at the cover of Gravitation: it shows ants crawling on an apple starting at its equator with their initial tangent vectors totally parallel to each other at the apple's equator. As they crawl forward, never changing direction in their own frame of reference, what happens if they cannot stop their own crawling, just as you cannot stop your own time from passing? They meet at the top of the apple! No force attracted them, they just followed their path through the apple's curved surface and bumped into each other, just as if some so-called "gravity" had attracted them.

I believe this view of gravity is much more accurate than the "force" view of it because all experiments to date confirm this much better accuracy. Namely, they have debunked Newtonian "gravitational force". No such thing exists. Moreover, increasing the precision of our measurements will not restore the understanding of gravity as a force like the true forces, but push even further away from it. That's why the idea of "unifying the 'four' 'forces'" is mathematically nonsense, and is either a lame attempt at popularizing science, or most physicists really need to learn some math. I don't know string theory and all the other "quantum gravity" fads, but if they really result from "unifying the four forces", they need to be thrown in the trash, and somebody really needs to start hitting the math books.

Answer 5

Gravity is a force. It looks like I have to enlighten people here again with another post before I leave.

The way to visualize the field for gravity as well as electromagnetic is this:

• Imagine the confine space as an aquarium. You have put the ink inside the aquarium. The denser the ink, the more gravity. This is the visualization of the curved space/path that light travels. A particle with mass has ink around it distributed in spherical manner. Any spherical surface with radius d has the same amount of ink, as the area of any spherical surface is proportion to squared distance, any field force has an inverse squared distance in formula. Objects with mass impact with the ink and moves to area with denser ink. The more particles with mass there are, the denser the ink/field in that area.

That is how you visualize the 4th dimension.

Now let's go to explaining inertial force. When you subjectively choose your frame of references if you don't choose the global frame of reference, you ignore the ink from all massive particles in the universe/global and include object in your local only. This means there is an absolute frame of reference, it is the frame of reference that takes into account the 'ink'/gravity of all massive particles in the universe. But we can't get to this level of absolution, so we really get relatively absolute. This means we only take into account the significant masses in our calculation and disregard the small ones. This is what happens when you choose the sun as the frame of references. You ignore the small distribution of ink/gravity from other stars and galaxies too far from the sun. You get computation that contains errors but still very accurate.

When one accelerates, if the one has mass, one interacts with the global distribution of gravity/field pulling one to the initial position (and this initial state of the whole system). This is the source of inertial force. It is real, and is regardless of your choice of frame of reference. Your choice of frame of reference is simply just how much from the global ink you want to ignore and accept as error in your computation. When the global ink is too much (mass of the earth, mass of the sun), you call the error inertial and take care of it in your computation as well.

This is also the mechanics to consistently reason about the twin paradox. You fix the frame of reference to the global frame of reference of all particles with mass in the universe, then one brother moves "more" and interacts with "more" ink/gravity than the "more" stationary one which interacts with "less" gravity. Twin paradox is consistently reasoned and is logical now. Absolutely relative can never reason about this basic phenomenon.

Answer 6

In the framework of GR, gravity is indeed not a force as it's a consequence of Newton's first law instead of the second one.

Each point in space-time comes with its own velocity space attached, and you need the parallel transport (and thus a connection aka gravity field) to be able to even define what you mean when you say a body moves without acceleration.

In the more general setting of arbitrary second-order systems (ie if we forget about Newton's laws), the space of acceleration fields carries an affine structure. A connection is one way to choose a zero point and make it into a vector space so you can have the notion of addition of forces (or rather acceleration fields). From this point of view, gravity would indeed be a force like any other, but special insofar as it gets chosen as the one that is called zero.

Answer 7

If gravity were a force, then there wouldn't be gravitational time dilation.

So let's assume gravity is a force, that pulls everything downward. We have a tower with one observer at the bottom and top.

The observer at the top drops two balls waiting $t$ between the two drops. The bottom observer would measure the very same time interval $t$ between the two falls.

But in reality there is difference between the two times, the bottom observer measures a smaller amount of time due to dilation. This effect is confirmed by many experiments. To have time dilation we need an accelerating frame of reference.

The reason of the time dilation is that the plane of simultaneity of an observer sweeps past other observers in a different rate than the rate of his clock.

In the following chart you can see an accelerating observer's worldline highlighted with blue (accelerating with constant proper acceleration). The radial lines are its planes of simultaneity at 0.2s, 0.4s, ... on his clock. The other hyperbolas are worldlines of points that remain rest at the frame of this observer, they are also accelerating but with a different rate. The red dots are the events when the clocks of each points hit 1s.

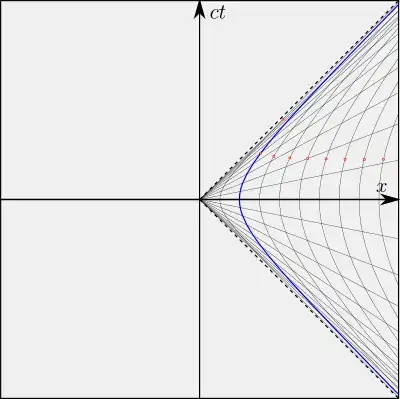
You can see when the blue observer's clock hit the 1s, at the same moment the clocks at the points on the right are passed 1 second long ago, while clocks at the left are lagging behind. No curvature needed to get dilation, just accelerate.

So to sum up, when you stand on the Earth, you are actually in an accelerating reference frame that accelerates upward, and gravitation is just a fictitious force, the same force you feel in a car or train, when it accelerates.

Then why Earth is not falling apart, if things are accelerating upward on it? Because the space-time is curved. It's curved so inertial observers falling towards the center of the Earth. But we who are "hovering" in this field are accelerating upwards in this curved coordinate system.

Answer 8

Newtons second law with his law of gravitation states for a test particle $m$:

$m_i\frac{d^2\vec{x}}{dt^2}=G \frac{m_g M}{r^2}\vec{e_r}$.

Where $m_i$ is the inertial mass and $m_g$ is the gravitational mass. From experiment it is known for a long time that $m_i=m_g$ (to extreme precission) but this means that the equation above is indipendent of the mass of the test particle: so its trajectory depends only on the mass M "generating the gravitational field" and initial conditions. So all object with the same inital conditions fall with the same speed (the old feather-coin-experiment).

This opens the possibility to describe gravitation as a geometrical property. In General Relativity trajectories of free falling particles are then geodesics (free motions) in the courved space generated by the mass M. In General Relativity there is no need for a gravitational force because the effect of the gravitational field is fully described via the courvature of the four dimensional space time. So in General Relativity there is no gravitational force in the classical meaning.

Maybe one last point towards "General Relativity vs Newtonian Physics": The Newtonian equation of motion and expression for the gravitational force is the exact low energy limit of the General relativistic geodesic equation. Meaning if you evole the expressions of General Relativiy for small masses/low energys you get the equations of Newtonian Physics. In that sense I would say the classical gravitational force is the low energy limit of the much more complex theory of gravitation. The classical gravitational force is not suited to describe all effects of gravity as a physical effect. At low energys/small masses Newtonian/classical physics does a fine job of describing our nature but at higher energys one needs Special and General Relativity to describe our nature/the experiments.

"What gravity realy is" is a physical question. Describing it with a force (in the classical physical sense) is not suited to describe nature as we see and measure it.

Answer 9

Einstien is right about one thing, gravity is not a force as defined by F=ma, but gravity is a force if you define force as resulting from energy.

Energy is hidden in the equation F=ma twice. Once in the Force and once in the acceleration. That is how energy is expressed in this equation. If motion is involved, energy is involved.

So is Einstein right about space-time curvature causing gravity? I don't know, but if it is space-time curvature, then the space-time curvature must be able to create energy.

"Force" is the result of energy acting on mass. "Mass" is defined by the weight of mass in gravity. Gravity is energy or a source of energy.

F=ma has an energy input which is "a" and an energy output "F"

If energy comes out of the equation, energy must go in, energy must be on both sides.

Mass is the medium used to calculate the energy in terms of acceleration, and it is the acceleration of gravity that is used for calculating "mass."

So energy in from gravity is expressed as constant acceleration. The product of energy and mass combined is what gives mass weight. The energy stored as weight can be transferred to another form of energy by necessary means. But gravity appears to be able to put energy into mass.

So if Einstein hasn't addressed the energy of gravity, he will have had a hard time understanding it. What ever the source of gravity, gravity is acceleration and not force. Force is mass by acceleration where as gravity is just acceleration.

The thing about that is all mass accelerates at the same rate, which generates different force on all things at all times with enormous variations in force resulting.

How can gravity be constant and yet apply unlimited numbers of force at any given moment? Gravity isn't a force, it is acceleration that generates force.

Same behavior is observed in electro-magnetic fields and explains many behaviors of gravity. If gravity's field is different, it is still related as it also explains gyroscopic effects. As you spin a metal mass, the centrifugal force creates a difference in charge from the outside and the inside of the spinning metal. By becoming charged, the metal aligns with the "field of gravity." Could be something different, but mass in gravity behaves a lot like mass does in magnetic fields.