How does the orientations of the two black holes' spins show up in LIGO data? (GW170104)

Question

Today's Phys. Rev Letter GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2 shows the analysis of the third confirmed detection of a black hole merger by the LIGO collaboration. According to the paper this even may differ from the previous two:

The black hole spins are best constrained through measurement of the effective inspiral spin parameter, a mass-weighted combination of the spin components perpendicular to the orbital plane, $\chi_{eff} = -0.12^{+0.21}_{-0.30}$. This result implies that spin configurations with both component spins positively aligned with the orbital angular momentum are disfavored.

You can see a simulation in this LIGO/Caltech video (which I found here), showing what I believe is precession of the tilted spin axis of one of the objects. https://youtu.be/S2vp7iVWrkE

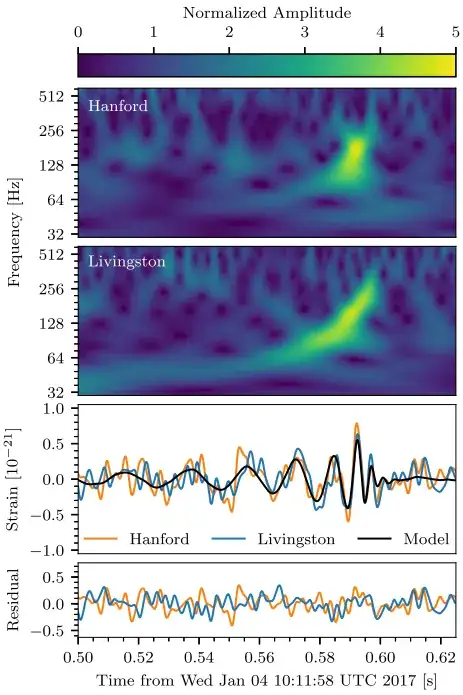
If I understand correctly, while there is significant pre-processing in frequency space, the final data for each site is really only the one-dimensional strain versus time plot, and all extracted parameters from the event come from the maximum-likelihood fitting of theoretically generated strain waveforms to these two plots for the two LIGO sites. See the several good answers to How were the solar masses and distance of the GW150914 merger event calculated from the signal? for further information.

A great deal of work has gone in to the statistical analysis of these events, both for low latency detection (alerts to the community for possible coincident optical detection) and more careful analysis later. The fact that $\chi_{eff}$ is so many error bars away from unity suggest there is a good chance the spins were not aligned to the orbit. In Section IV. at the bottom of the first column on page 221101-4 it says for example:

Considering the two spins together, the probability that both tilt angles are less than 90° is 0.05

Question (Edited): How does the alignment of the spins manifest itself in the waveform shown in the LIGO data? Is it a subtle shift in phase near the end, or a modulation of amplitude?

Are there any examples of a simulated waveform for very different values of $\chi_{eff}$ that show the difference?

above: Enlarged, cropped section of Figure 1, shown below.

above: Figure 1.

Answer 1

$\chi_{eff} = (m_1S_{1z} + m_2S_{2z})/(m_1+m_2)$ is a measure of how the z-component of the spins is aligned with the orbital angular momentum. The term which affects the evolution of binary after quadruple (Newtonian) term depends on a combination of $\chi_{eff}$ and mass ratio. Newtonian term depends on the chirp mass of the binary. So you can measure chirp mass fairly accurately but you can only measure a combination of $\chi_{eff}$ and mass ratio. Coming on to how aligned projection of spin effects the evolution of binary here is a nice plot showing it. If both the spins are aligned with the angular momentum then binary takes longer to merge and vice-versa if they are anti-aligned. The business with precession is very different. If the spins are not aligned with the angular momentum then the waveform modulates. Off-course it depends on from where are you looking at the binary. If you are looking from the edge the modulation is most. Something like this. Currently LIGO searches are not including precession when they search for gravitational waves. A face-on binary will show no precession so no one is caring for it right now (off-course this is purely search sensitivity based argument - an edge-on binary is seen to distances much smaller than face-on binary) but observation of prescessing binaries will be great.