1

I'm currently reading through a hydrodynamics lecture course and I'm confused at some of the key integrals that are derived. These integrals aid in deriving the moments of the Boltzmann equation.

First, the moments are:

$\int\big(\frac{\partial f}{\partial t}+v_j\frac{\partial f}{\partial x_j}+a_j\frac{\partial f}{\partial v_j})d^3\textbf{v}=0$,

where $f=f(x,v,t),\;d^3\textbf{v}=dv_1dv_2dv_3,\;v=\dot{x},\;a=\dot{v}$ and this equation is calculated three times with different factors: mass, momentum and energy $(m, mv, mv^2/2)$

Using the velocity moments of the the distribution function $f$ I can only get the first part of the integral, where $f$ is only differentiated by time, while the others are a bit more confusing, because I can't get the result they present.

E.g. they suggest that

$\int\frac{\partial f}{\partial v_i}d^3\textbf{v}=0$

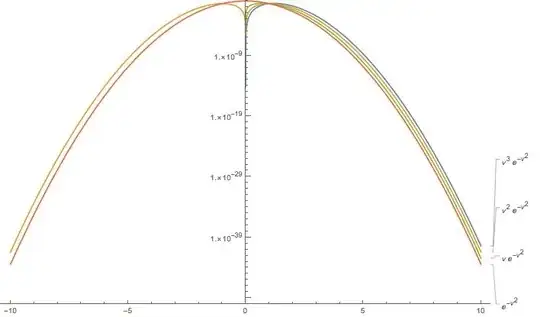
if we just integrate by parts and the fact that since the total mass/momentum/energy must be finite then f must follow this condition, which I'm not sure where it comes from:

$\lim_{v \to \infty} v^2f=0$

That is my main problem, the other integrals seem more manageable, but

$\int\frac{\partial f}{\partial v_i}d^3\textbf{v}=0$

is difficult to understand.

The other integrals are:

$\int v_j\frac{\partial f}{\partial v_i}d^3\textbf{v}=-\delta_{ij}\frac{\rho}{m}$

$\frac{1}{2}\int v^2_j\frac{\partial f}{\partial v_i}d^3\textbf{v}=-\frac{\rho}{m}u_i$

I'm less worried about them since I believe that with understanding that one integral that I asked about above the rest would follow logically.

honeste_vivere
  • 16,028
Tigs
  • 121

1 Answers1

2

E.g. they suggest that $\int \ \partial f/\partial v_{i} \ d^{3}v = 0$ if we just integrate by parts and the fact that since the total mass/momentum/energy must be finite then f must follow this condition, which I'm not sure where it comes from: $\lim_{v \rightarrow \infty} v^{2} \ f = 0$

If $f\left( \mathbf{v} \right)$ is a velocity distribution function and we know that $f\left( v \right) < \infty$ must be true (i.e., there cannot be an infinite number of particles per unit phase space), then it must follow that: $$ \lim_{v \rightarrow \infty} v^{2} \ f \propto \lim_{v \rightarrow \infty} v^{2} \ e^{-v^{2}} \rightarrow 0 $$ assuming a Maxwellian velocity distribution.

This can be seen when one plots this versus speed (see below).

If you are confused about the integration by parts step (e.g., $\int \ u \ dv = u \ v - \int \ v \ du$), then recall that for a Maxwellian (1D for brevity): $$ \frac{ \partial f }{ \partial v } = f_{o} \frac{ \partial }{ \partial v } \ e^{-v^{2}} = -2 \ v \ f $$ Thus, the $v \ u$ term (expression from Wikipedia link above) goes to $\sim v^{2} \ f$ which is then evaluated at the limits of the original integral (i.e., $\pm \infty$). You know that any terms with odd powers of $v$ will go to zero under integration (i.e., negative values of $v$ result in negative values for the function) so the $\int \ v \ du$ term also goes to zero. v^n-Gaussians vs. Gaussian

Side Note: The velocity moments can be derived in a slightly different manner, where one knows that the units of $f\left( \mathbf{v} \right)$ are number per unit length cubed per unit velocity cubed. Thus, just from dimensional analysis (or physical reasoning), one can argue that the following must be true: $$ n_{s} = \int_{-\infty}^{\infty} \ d^{3}v \ f_{s}\left( \mathbf{v} \right) $$ where $n_{s}$ is the number density (i.e., number per unit volume) of species $s$.

I wrote a more detailed answer and discussion of velocity moments at https://physics.stackexchange.com/a/218643/59023.

honeste_vivere
  • 16,028