How do I derive Lorentz transformations from $S^2=c^2t_1^{\,2}-v_1^{\,2}t_1^{\,2}=c^2t_2^{\,2}-v_2^{\,2}t_2^{\,2}$

Question

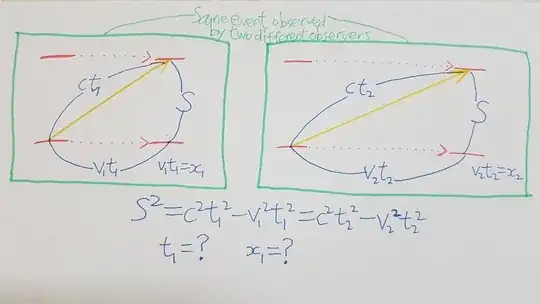
As in the picture, a typical vertical light clock is moving to the right at $v_1$ for one observer and at $v_2$ for the other observer. How do we derive full Lorentz transformations from this?

Answer 1

One possibility is to substitute the $t_i$ with an imaginary time: $t=i\tilde t$. If you plug this into your interval, it becomes euclidean: $$ds^2=c^2dt^2-dx^2=-c^2d\tilde t^2-dx^2$$ You know that the euclidean norm is invariant under rotations, so you can claim that the transformation matrix in these new coordinates $(c\tilde t,y)$ is just the usual rotation matrix. After some maths and pushing the $i$'s around, you will get that the original coordinates $(ct,x)$ transform with pseudorotation matrices. To get how the pseudorotation angle $\psi$ is related to the relative velocity between coordinate frames $v$, calculate the velocity addition law, that is, calculate $\frac{dx'}{dt'}$ in terms of $\frac{dx}{dt}$ and $\psi$. You should get from it that $$\tanh\psi=-v$$ I have worked out these calculations on paper but don't have it TeXed, that's why I don't provide the worked out calculations, but let me know if you get stuck somewhere!