Derivation of the capacitance of a cylindrical capacitor

Question

I have started learning about the capacitance of the capacitors of various geometries from my textbook. While calculating the capacitance of a parallel plate capacitor, the formula

$$ V_f-V_i=-\int^{f}_{i}\vec E\cdot d\vec s$$

was modified for the present situation as

$$ V=\int^{+}_{-}E\ ds$$

as path of integration starts on the negative plate and ends on the positive plate , opposite to the direction of electric field.

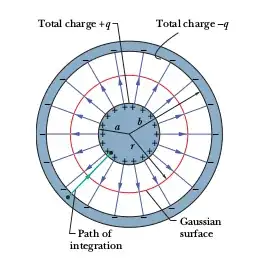
Now below is a part of the method of calculating the capacitance of a cylindrical capacitor from the same text (Fundamentals of Physics, by Halliday, Resnick, and Krane):

 As a Gaussian surface, we choose a cylinder of length $L$ and radius $r$, closed by end caps and placed as is shown in Fig. 25-6. It is coaxial with the cylinders and encloses the central cylinder and thus also the charge $q$ on that cylinder. Equation 25.4 then relates that charge and the field magnitude $E$ as $$ q=\epsilon_0EA=\epsilon_0E\left(2\pi rL\right),$$

in which $2\pi rL$ is the area of the curved part of the Gaussian surface. There is no flux through the end caps. Solving for $E$ yields: $$ E={q\over 2\pi\epsilon_0 Lr}. \tag{25-12} $$

Substitution of this result into Eq. 25-6 yields

$$ V=\int^{+}_{-}E\ ds=-{q\over 2\pi\epsilon_0L}\int^{a}_{b}{dr\over r}={q\over 2\pi\epsilon_0L}\ln\left({b\over a}\right), \tag{25-13} $$

where we have used the fact that here $ds=-dr$ (we integrated radially inward).

What I don't understand is why we are again taking $ds = - dr$ as we already did that while modifying the below equation.

$$ V_f-V_i=-\int^{f}_{i}\vec E\cdot d\vec s$$

Answer 1

Recall that the definition of electric potential in terms of electric field is

$$ V = - \int_{\infty}^{r} \vec E \cdot d\vec s$$

where we are defining the potential to be zero infinitely far away. In this problem, you simplify the integrand to be $E \cdot ds$ since you know that their vectors are radially-parallel. The other modification you make is that, instead of integrating from zero-potential to $r$, you integrate from $r$ out to zero-potential. This switches the limits of integration, and removes the negative sign, which you have already done in your question.

In this problem, however, you only have to use this equation once. You first use Gauss' law to find the electric field, and then you apply this integral to get the electric potential.

Answer 2

I don't think you would need to integrate radially inward specifically, but what is required is to integrate radially. You can take $dr=ds$, this will mean you are integrating along the field, i.e. outward instead of the opposite that is done in the book. Here's the thing if you integrate by taking $dr=ds$, the final result is $$ V= \frac{-q}{2 \pi \epsilon L}. ln(\frac{a}{b}) $$

If you understand logarithms, this would be the same as

$$ V= \frac{q}{2 \pi \epsilon L}. ln(\frac{b}{a}) $$

,which is given in the book, because $ b>a $

If you take this equation,

$$ V= \int_-^+ E\,\,ds $$

You are integrating from negative plate to positive plate, which means that the infinitesimal distance $ds$(its direction has already been considered to get to this equation) goes opposite to field and thus opposite to the radial vector $ d\vec r$.

The original equation is,

$$ \Delta V= - \int_-^+ \vec E . d\vec r $$ Start with this equation and you will find that taking $ dr=ds $ with this equation is equivalent to taking $ dr = -ds $ with the previous equation.