About the reason why the change of a muon into an electron plus a photon is not seen

Question

Let me state first that I don't think this is a duplicate of the mentioned question, though the basic thought is the same. Nevertheless, I come up with the prequark rishon theory of Harari, which accounts for all interactions, and not with a muon that consists of an electron and two neutrinos. In the first answer to the abovementioned question, it is confirmed that muons (or quarks and leptons in general) could actually have a substructure. To reveal the substructure of leptons you could smash them together at very high energies (because it is known they exhibit no substructure if we probe them above a very little distance). I don't know if such experiments are done because in the framework of the standard model there is no need for them: it describes leptons (and quarks) as elementary, so why look for substructure if they are considered not as a composite?

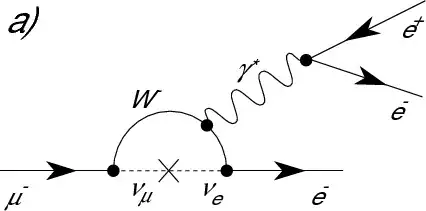
A muon (${\mu}^-$) changing into an electron ($e^-$) and a photon ($\gamma$), has never been observed in Nature (or maybe it's better to say " in particle accelerators"). To explain this, physicists assumed that there are two kinds of neutrinos: one associated with the electron (${\nu}_e$) and one associated with the muon (${\nu}_{\mu}$). They assigned a "muon number" $+1$ to the muon and its associated neutrino (and a value $-1$ to their anti-particles), and an "electron number" $-1$ to the electron and its associated neutrino (and value $+1$ to their anti-particles). These numbers had to be equal for the original particle and the particle into which it changes.

So a ${\mu}^-$ changing into a $e^-$ and a $\gamma$ (which obviously has lepton number $0$) won't occur because the muon number (and the electron number) has to be conserved (you can say it's an extension of the conservation of lepton number), which obviously isn't the case.

On the other hand, a ${\mu}^-$ can change into a $e^-$, a ${\bar{\nu}}_e$ and a ${\nu}_{\mu}$, which you can check by inspecting the (additive) muon and electron numbers for the particles.

With this rule (conservation of electron number and muon number, to which we can nowadays add a tau number) you can predict which changes can take place.

But is this really a explanation why the ${\mu}^-$ can't change into a $e^-$ and a $\gamma$?

I suppose not, so what is the conventional, deeper explanation (in the framework of the standard model) that this change can't take place?

And can't we just as well say that the $\mu^-$ is composed of three particles which each carry an electric charge (amongst other kinds of charge) of $-{\frac 1 3}$, so, because of the repulsive force of these charges, the ${\mu}^-$ can't change into $e^-$ because in a $e^-$ the three charges are closer to each other (which would require the absorption of a photon)?

Answer 1

The diagram in the answer by the OP does not conserve lepton number.

Conservation of lepton number is one of the experimental facts which gave rise to accepting the standard model , SM, as the basic model of particle physics .

It is known that there exist experimental facts which are not within the SM and need an extension of it, for example CP violation in the model is not enough to explain cosmological data. Neutrino oscillations are not included in the SM because there their masses are assumed to be zero and an extension of the SM is needed.

A neutrino oscillation correct Feynman diagram, within a reasonable extension ( consistent with the rest of the data) of the standard model will allow for the reaction to happen , and is this one :

neutrino oscillation is indicated by the cross. For the OP's channel reduce the number of vertices by eliminating the e+e- pair.

There are also other diagrams possible in Grand Unified theories, or Super symmetries that allow for the possibility of the channel under discussion .

When looking for extensions of the SM one has to embed it, i.e. follow the main structure , because the SM is an encapsulation of an enormous amount of data, and any ad hoc additions will most probably violate something that is supported by a lot of data. If , as in the proposed by the OP diagram , Z exchanges could go with lepton number violation, a lot of unusual channels would have opened at LEP, which were not seen. There would not have been a lepton number rule and there would have been a different standard model.

Note that the diagram above still depresses the probability at low energies for the decay channel, as the OP diagram, but at LEP energies a lot of violations of lepton numer would have been seen if the diagram of the OP were correct..

Answer 2

There is no reason to suppose that electrons or muons are anything other than purely fundamental at the present time. There are strong upper limits on the radius of an electron, and no structure of multiplets of particles that you'd associate with such a composite structure, as led to the quark model of hadrons.

In the standard model the particles are organised into three generations. Each generation is like a pattern of particles; all three generations have the same basic pattern, but repeated with successively heavier particles. The statement that a muon is 'like the electron's heavier brother' becomes that the electron and muon are in different generations (and in the third generation, there is a tau particle that plays the same role).

In each generation, together with the charged lepton (i.e. The electron or muon or tau) there is a neutrino; the charged lepton and corresponding neutrino can change into each other with the emission or absorption of a charged W boson. This boson can then decay into a (lighter) charged lepton and neutrino. So the rules for what particles can turn into each other are set by the pattern within each generation, but the gauge bosons talk to all the generations.

Answer 3

The Feynman diagram associated to the muon which changes in an electron and a photon would look like this:

In this diagram, the particles in the triangle are the virtual particles, while the lines for the incoming muon and the outgoing photon and electron represent the real particles.

Now for the change not to occur, this Feynman diagram should give a zero amplitude for the process of the muon changing into an electron and a photon. It's a straightforward but long calculation, but I can tell you that without actually computing it the amplitude is (for sure) 0, so the process won't occur.