1

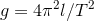
The title may seem a bit off topic. I will explain my doubts with an example. Let there be a situation where we are measuring gravity using the formula enter image description here

Now, if the least count or error in the measurement of $l$ and $T$ is given, I can easily find the net error or relative error by taking a natural log on both the sides of the equation and differentiation.

But how to include the number of trials? For example, I learned somewhere that if the least count of a stop watch is 1 second, and the number of trials, say to measure the oscillation period of a pendulum is 20, then should the error in measuring the time period be cut down to 1/20 seconds?

Qmechanic
  • 220,844
MrObjectOriented
  • 281

1 Answers1

3

There's two possible things going on in such a measurement:

a) measure the time taken for $n$ oscillations and then your systematic error will indeed be reduced, e.g. minimum stopwatch interval $ / n$; and

b) do the $n$-oscillation measurement $N$ times to estimate the statistical uncertainty.

As described by the answers at How to combine measurement error with statistic error (thanks to Emilio for the link), these error sources should be added in quadrature. The statistical error will converge to zero as $N \to \infty$, but the systematic limitation on $T$ remains fixed... unless you make $n$ bigger, assuming that $T$ remains constant through a long "run".

andybuckley
  • 210
  • 2
  • 9