7

According to E. Chabanat et al. (1997), the speed of sound in a nuclear medium is defined as

$$\left(\frac{v_s}{c}\right)^2 = \frac{dP}{de}$$

with

$$P = \rho^2 \frac{dE/A}{d\rho}$$ and $$e = \rho\left(mc^2 + \frac{E}{A}\right).$$

  1. First request: I was wondering if someone could explain me how we derive this expression.

  2. Second request: I know that the speed of sound will be huge in neutron star comparing to the speed of sound in air but I don't know why this quantity is interesting in nuclear astrophysics studies.

Qmechanic
  • 220,844
T. Auerrac
  • 138

1 Answers1

4

The speed of sound is an important property of an equation of state (EoS): depending on the setting for various reasons.

In the context of neutron star (NS)/ nuclear EoS the speed of sound is a measure of stiffness of an EoS: a stiff EoS (an EoS with a high sound velocity) generates a high pressure at given energy density. In order to allow for massive ($M>M_\odot$) NS the EoS needs to be rather stiff: to form massive compact objects the EoS needs to be able to generate large pressures to compensate for the strong gravitational attraction. Lets consider a very simple EoS: an EoS with a constant speed of sound $c_s$: $$\epsilon=\frac{P}{c_s^2}+\epsilon_0 \Longleftrightarrow \frac{d P}{d\epsilon}=c_s^2.$$ I use geometrized units with $c=G=1$ in which the speed of sound is dimensionless and measured in fractions of the speed of sound $c$ so $c_s=1/3$ in SI units is $\sim 10^8 \mathrm{m s^{-1}}$.

The following figure shows mass-radius and mass-central pressure curves for three different EoS. The data points of this figure correspond to solutions of the general relativistic structure equations of hydrostatic equilibrium (TOV equations). I matched those constant speed of sound EoS to a realistic low density curst EoS to get NS with realistic radii.

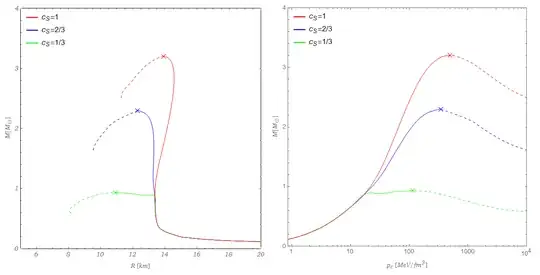
M-R and M-p_c curves

The crosses denote the maximum mass obtainable with the respective EoS and the dotted lines are unstable configurations. So we can clearly see that we need very stiff/high sound velocity EoS to get stable stars with masses above $2M_\odot$. The red line corresponds to NS with an EoS at the causal limit $c_s=1$. With such a stiff EoS we can get stable NS with masses up to $\sim 3.2 M_\odot$.

A realistic NS EoS for the high density regime needs to be rather stiff to allow for $2M_\odot$ NS but it also needs to be causal so $c_s<1$. For most purely nuclear EoS the speed of sound is not constant but density dependent.

So far I only talked about the impact of the sound speed on masses and radii of NS but it is also important for many other things: Deformability, dynamic stability, quakes, transport properties all strongly depend on the EoS and its speed of sound. It is also a quite interesting parameter for Quark matter EoS and hybrid NS (NS containing hadronic and Quark matter). Maybe one short note on this: the asymptotic freedom of QCD suggest that Quark matter at very high densities behaves like a free ultra relativistic gas with a constant speed of sound of $c_s^2=1/3$.

In terms of a derivation of the expression for $c_s$: it can be derived from the relativistic Euler equation $\nabla_\mu T^{\mu\nu}=0$ and the continuity equation projected into the fluid rest frame. [S. Yoshida, 2011, Dummy’s note (5): Sound speed in relativistic fluid] gives a short derivation of the expression for the speed of sound an the corresponding wave equation.

N0va
  • 3,109