Why do two objects traveling at the speed of light not collide at 2 times the speed of light?

Question

I was watching a Brian Cox lecture, and he touched upon the notion that if two objects were moving towards eachother at the speed of light and collided, they would collide at no greater than the speed of light, when they should collide at twice the speed of light I believe. Why is this?

Answer 1

(This answer elaborates on the comment from @Armando .)

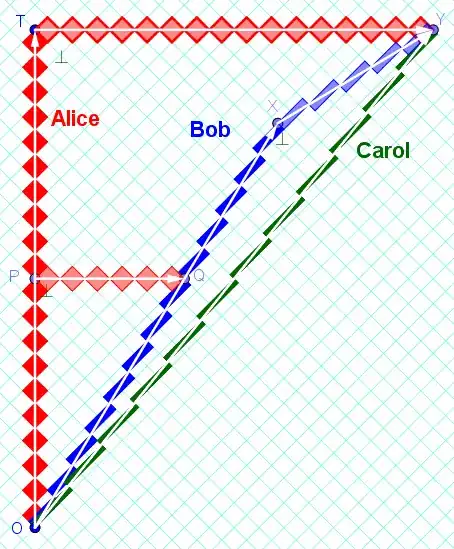
Consider this spacetime diagram on rotated graph paper.

Alice uses Minkowski-right triangle OPQ, with right-angle P and legs parallel to her axes to declare that Bob has velocity $v_{BA}=6/10$ with respect to Alice. (Any triangle similar to OPQ could be used to determine this velocity.)

Bob uses Minkowski-right triangle OXY, with right-angle X and legs parallel to his axes to declare that Carol has velocity $v_{CB}=5/13$ with respect to Bob.

So, what is the velocity of Carol with respect to Alice?
Alice uses Minkowski-right triangle OTY, with right-angle T and legs parallel to her axes to declare that Carol has velocity $v_{CA}=16/20$ with respect to Alice.

These velocities are related by the velocity composition formula $$\begin{align}v_{CA} &=\frac{v_{CB}+v_{BA}}{1+v_{CB}v_{BA}}\\ &=\frac{(\frac{5}{13})+(\frac{6}{10})}{1+(\frac{5}{13})(\frac{6}{10})}=(\frac{4}{5}) \end{align}$$ (This is the equation used by @NoethersOneRing .)

The Euclidean analogue of this is asking how "slopes" "add [compose]".
Geometrically, angles add... and slopes are equal to the tangent-function of the angle... but slopes don't add.
In special relativity, using the Minkowski-angle [the rapidity $\theta$, where $v=\tanh\theta$ and $\gamma=1/\sqrt{1-v^2}=\cosh\theta$], we have $$\begin{align}v_{CA}=\tanh_{CA} &=\tanh(\theta_{CB}+\theta_{BA})\\ &=\frac{\tanh\theta_{CB}+\tanh\theta_{BA}}{1+\tanh\theta_{CB}\tanh\theta_{BA}}\\ &=\frac{v_{CB}+v_{BA}}{1+v_{CB}v_{BA}}\\ \end{align} $$

So, in this example, (using a calculator or WolframAlpha) $$v_{CA}=\tanh(\rm arctanh(5/13) + arctanh(6/10) )=4/5.$$

For the speed of light case, $$v_{CA}=\tanh(\rm arctanh(1) + arctanh(1) )=1,$$ which implicitly uses $\infty+\infty=\infty$.

[In Galilean relativity, Galilean-angles add and slopes [i.e. velocities] add. Unfortunately, our common-sense has brainwashed us into thinking that velocities always add.]