Symmetry of spectrum of tight binding model with quasiperiodic potential

Question

In the Aubry-André model, a tight binding model with nearest neighor hopping and a cosine-like potential $\lambda_n = \lambda \cos(2\pi \beta n)$ (where $n$ is the lattice site, $\lambda$ is the potential strength and $\beta$ is typically irrational), it turns out that the spectrum is symmetric with respect to the energy zero. The model can be defined as $$ E a_n = a_{n+1} + a_{n-1} + \lambda_n a_n, $$ where $a_n$ is the component of the wave function at lattice site $n$, so the terms $a_{n \pm 1}$ describe the nearest neighbor hopping, and $E$ is the energy eigenvalue.
This can as well be understood as the problem to find eigenvalues $E$ and eigenvectors $\{ a_n \}$ of a matrix of the type $$ \begin{pmatrix} \lambda_{-2} & 1 & & & 1\\ 1 & \lambda_{-1} & 1 & & \\ & 1 & \lambda_0 & 1 & \\ & & 1 & \lambda_1 & 1\\ 1 & & & 1 & \lambda_2\\ \end{pmatrix} $$ where $\lambda_{-n} = \lambda_n$. This example shows the matrix for system size $5$ but I hope you get the scheme. The values $1$ in the off-diagonal corners show that periodic boundary conditions are applied, but I don't think this should be important from now on.
Now the symmetry of the spectrum basically means, that if there is a solution $\{ a_n \}$ with energy $E$, then there also exists another solution $\{ \tilde{a}_n \}$ with energy $-E$.

How would one show that this is true? The reason I want to do this is because another tight binding model including also next nearest neighbor hopping and a modified potential, $$ E a_n = a_{n+1} + a_{n-1} + t_2 (a_{n+2} + a_{n-2}) + \lambda_n a_n $$ with $\lambda_n = \lambda (\cos(2\pi \beta n) + t_2 \cos(4\pi \beta n))$ does not have a symmetric spectrum, so I thought that this might be a starting point to understand the difference between the spectrum of the two models. Better ideas are welcome, though. ;-)
Also, I don't know why this other model has a tendency to have overlapping bands but the Aubry-André model doesn't (see this paper by Magnus Johansson). Help on this would be appreciated as well.

Here's a plot of the spectrum of the Aubry-André model for a system of size $233$ with $\beta = 144/233$ (ratio of consecutive Fibonaccis numbers, converging against the inverse of the golden mean, just in case you were wondering why I use a rational value of $\beta$). You can see the symmetry:

---

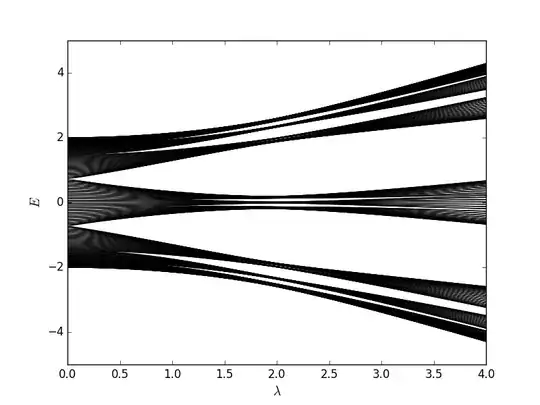
UPDATE 1: Here's a plot of the spectrum of the second model, also including next nearest neighbor hopping, for the same system size and choice of $\beta$. The hopping parameter $t_2$ for next nearest neighbor hopping is chosen to be $0.3$ here. As you can see, this is a total loss of the $E \leftrightarrow -E$ symmetry. Already at zero potential, the dispersion becomes $E(k) = 2 \cos(k) + 2t_2 \cos(2k)$ and the spectrum therefore loses the symmetry.

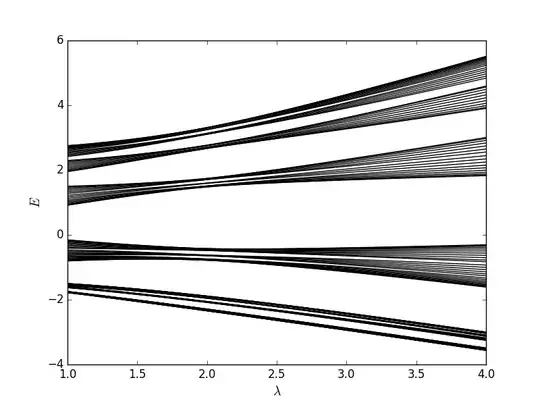
So you see there's a lot of difference between the band structures of the two models (symmetry, band overlap) even though their Hamiltonians are not so different ($t_2$ typically small, say less than $1/2$; self duality retained). I hope you can help me understand this. There's a lot of literature on the Aubry-André model and a few papers about the other model, but they mostly focus on the localization properties of the eigenstates and very little attention is paid to the spectrum. Numerically it is no problem to observe the above mentioned things, but it would be nice to have a more analytical approach to understand the difference of the models.

---

UPDATE 2 (2017-05-05): The paper mentioned above states that the model has a tendency to have overlapping bands and I didn't understand the reason for that. Now this paper chooses $t_2 = 1/3$ to be fixed. If one plots the dispersion relation at zero potential $E(k)=2\cos(k)+2t_2\cos(2k)$ for $0 \leq k \leq \pi$, one finds that for $t_2>1/4$ there's degeneracy in the low energy regions of the spectrum therefore giving band overlap. Here this can easily be seen in the plots of the sprectrum while for smaller values of $t_2$ I only found avoided crossings. So it might be that the author of this paper was referring to the special case of $t_2 = 1/3$ while I mistakenly thought he was talking about the general case of $t_2 \neq 0$ which I'm interested in.

Answer 1

The Aubry-Andre model only has exact $E\leftrightarrow -E$ symmetry in the thermodynamic limit or for particular rational choices of $\beta$. The easiest way (in my opinion) to see this is from the second quantized Hamiltonian: $$ \mathcal{H} = \lambda\sum_{n} \cos(2\pi\beta n)c_n^\dagger c_n + \sum_{n} (c_{n+1}^\dagger c_n + \mathrm{h.c.}) $$

Fourier transforming only the hopping term using $c_n = \frac{1}{\sqrt{L}}\sum_m e^{\mathrm{i} 2 \pi \beta n m} \tilde{c}_m$, you get the Hamiltonian in a form that clearly demonstrates the self-duality of the model: $$\mathcal{H} = \lambda\sum_{n} \cos(2\pi\beta n)c_n^\dagger c_n + 2\sum_{m} \cos(2\pi\beta m)\tilde{c}_m^\dagger \tilde{c}_m$$

Note that this only works for periodic boundary conditions with $\beta$ divisible by $L$ (system size) as you have in your example.

The $E\leftrightarrow -E$ symmetry is just saying that the Hamiltonian is equal to negative itself, up to some unitary transformation: $\mathcal{H} = -U\mathcal{H}U^\dagger$. Observe that $$ \begin{eqnarray} -\mathcal{H} &=& \lambda\sum_{n} \cos(2\pi\beta n + a\pi)c_n^\dagger c_n + 2\sum_{m} \cos(2\pi\beta m+b\pi)\tilde{c}_m^\dagger \tilde{c}_m \\ &=& \lambda\sum_{n} \cos(2\pi\beta (n + a/2\beta))c_n^\dagger c_n + 2\sum_{m} \cos(2\pi\beta (m+b/2\beta))\tilde{c}_m^\dagger \tilde{c}_m \end{eqnarray} $$ for any odd integers $a,b$. Therefore, you can see that flipping the sign of $\mathcal{H}$ is the same as just translation in real space by $a/2\beta$, and in momentum space by $b/2\beta$. When these two translations can be chosen to be integer, then this can be encoded as a unitary and is therefore an exact symmetry.

In your case, $a/2\beta = 233a/288$, which cannot be made integer with odd $a$ (and so does not have this symmetry exactly). For the previous Fibbonacci pair, $\beta = 89/144$ and therefore $a/2\beta = 72a/89$ which can be made integer with $a=89$, and so does have this exact symmetry.