3

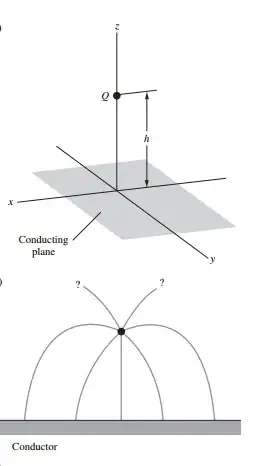
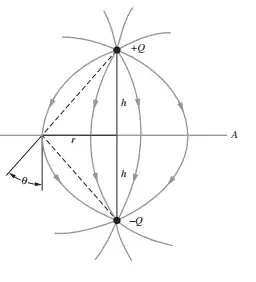
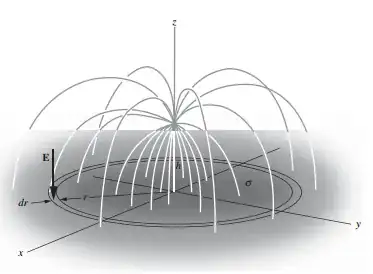
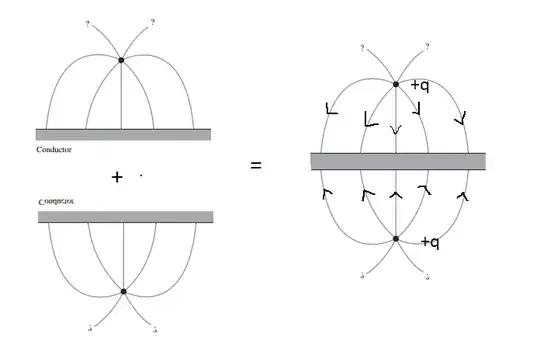
This kind of a configuration struck me when I read this question.

The original question asked how the force on the two charges would change if a metal plate was inserted between them. This question addresses what would happen if it was an infinite plane (those are so much more convenient).

I gave it some thought and the result is rather interesting.

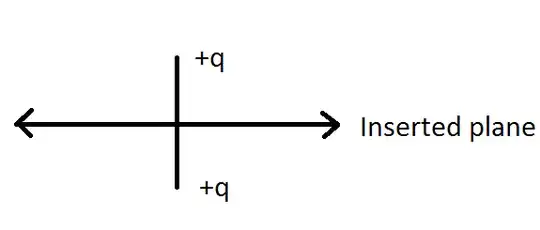enter image description here EDIT: This question is very different from the original in that:

  • The infinite plane is grounded, a plate with definite dimensions does not have to be
  • One can't use image charges with the plate
  • If the plate is uncharged, positive charges will accumulate on the edges and create their own field, in case of an infinite plane these positive charges are at infinity and do not affect the configuration.
  • A plate does not provide electrostatic shielding or a simple boundary region to apply the uniqueness theorem in.
  • The charge distribution on a finite plate is much harder to model.
Community
  • 1
GeeJay
  • 1,660

1 Answers1

3

Let's say the conducting plane is the x-y plane. One charge is in the $+z$ half and the other in the $-z$ half.

Let's focus on a configuration that consists of just the charge in the top half and the conducting plane. For a point charge $q$ above a conducting plane, the charge distribution on the plane can be found from the image charge method (this is very well illustrated in chapter 3 of Purcell's Electricity and Magnetism).

The sum of the fields due to the plate and $+q$ is zero for $z<0$. For $z>0$, the electric field is like that of a dipole.

The image charge method will also tell you that the force on the charge $+q$ is that of an image charge $-q$ at the same distance from the xy plane but in the bottom half.

enter image description here

enter image description here

enter image description here

Now let us consider just the charge in the bottom half and the conducting plane. The field is going to be just the opposite of what was described above. Zero for $z>0$ and that of a dipole for $z<0$. Now using the superposition theorem, we can put these two configurations together.

What is most fascinating here is that the field due to one charge does not penetrate into the region with the other charge. This is electrostatic shielding. So the force on each positive charge is as if there was a negative charge of the same magnitude where the other charge is sitting.

When you sum this up it's a truly astounding result: if there are two positive charges and you insert an infinite conducting plane between them, the force on either charge changes sign!

enter image description here

*All images from Purcell's Electricity and Magnetism

Community
  • 1
GeeJay
  • 1,660