Conservation of angular momentum in Euler's equation

Question

Consider the following equations

\begin{align} I_1 \frac{dΩ_1}{dt} + (I_3 - I_2)Ω_2 Ω_3 &= K_1, \\ I_2 \frac{dΩ_2}{dt} + (I_1 - I_3)Ω_3 Ω_1 &= K_2, \\ I_3 \frac{dΩ_3}{dt} + (I_2 - I_1)Ω_1 Ω_2 &= K_3. \end{align}

According to this equation if external torque is zero,then the following results occur

\begin{align} I_1 \frac{dΩ_1}{dt} + (I_3 - I_2)Ω_2 Ω_3 &= 0, \\ I_2 \frac{dΩ_2}{dt} + (I_1 - I_3)Ω_3 Ω_1 &= 0, \\ I_3 \frac{dΩ_3}{dt} + (I_2 - I_1)Ω_1 Ω_2 &= 0. \end{align}

Here $K_1,K_2,K_3$ are torques and $I_1,I_2,I_3$ are moments of inertia.

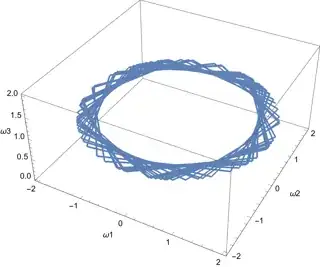
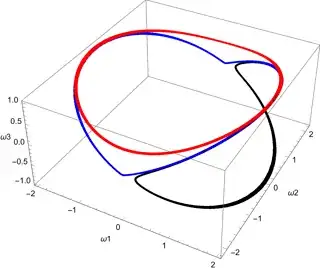
I used Runge-Kutta 4th order method to predict the angular velocity and used the Euler equation to calculate the rate of change of angular velocity (for Runge-Kutta method). But after observing the plot of energy after looping this method for some amount of time (say 50000 seconds), the energy was not conserved. There is a decrease in amount of energy. I am not sure what is causing this decrease in energy. Is the angular momentum not conserved according to the equation?

Answer 1

The angular momentum is conserved by this equation because it is derived from $$ \frac{\rm d}{{\rm d}t} \mathbf{L}_C = \sum \boldsymbol{\tau} $$

_{See Derivation of Euler's equations for rigid body rotation post for details. The derivative of angular momentum is zero when the torques are zero and thus $\mathbf{L}_C$ is constant.}

I think the most likely scenario is that the numeric method will not conserve total energy, neither will it conserve angular momentum. There are some integration methods (called symplectic) that do conserve those quantities and Runge-Kutta is not one of them.

PS. NASA published an analytic solution to the above problem for some special cases (see this pdf report) and those analytic solutions do conserve angular momentum.

Answer 2

I actually checked. Of course $50000$ seconds depends on your timescale and on your values for $\vec \omega$. I chose $(\omega_1(0),\omega_2(0),\omega_3(0))=(2,0,1)$ and used $I_2=2, I_3=1$ and variable $I_1$. I got the kinetic energy $$ 2T_{rot}= \sum_k I_k\omega_k^2 $$ to be conserved all the way to $t=50k$ using a variety of methods. However, I do not quite trust some qualitative features of the numerical solutions.

For instance, with $I_1=I_2=2$, one should obtain a simple precession about the third axis. While my schemes show that $L_3=I_3\omega_3(t)$ is indeed constant, the other two values of angular momentum to not remain exactly on a circle but rather seem to oscillate, as you can see from the figure, with $\vec\omega(t)$ plotted to $t=250$.

On the other hand, there is a critical value $$ I_{1c}=\frac{I_2}{2}+\sqrt{\frac{I_2^2}{4}+I_3(I_2-I_3)\left(\frac{\omega_3(0)}{\omega_{1}(0)}\right)^2}\, . $$ which separates two types of motion. For my values this works out to be $I_{1c}=2.11803$. Taking the values $I_1=2.08$ and $2.12$ on either side of this critical value gives "good" curves of $\vec\omega(t)$ up to $t=2500$, as you can see below. The blue curve is very nearly the separatrix and was obtained using $I_1=2.118$; the red and black curves correspond to $I_1=2.08$ and $2.12$ respectively.

All of these were obtained using Mathematica and forcing the Method to RK of difference order $4$. Thus I suspect it's likely to be your integrator that is buggy.