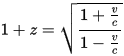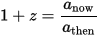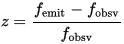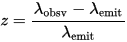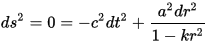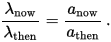In a gravitational field it is a General Relativistic (GR) effect. For the cosmological solution to GR, it is due to the metric components changing over time, and using comoving spacetime (moving with the average cosmic flow) one can express it as dependent on the universe scale factor ratio (from when received to when transmitted), and so we say it is due to the expansion of the universe (which is the scale factor increasing over time).
In straightforward terms, yes, it is the expansion of spacetime that causes the wavelength (the physical distance between crests, say) to increase. Just as the physical distance between far-off galaxies increases. The wave property is a real property of a photon, and its peaks or crests are real. One measures that.
REDSHIFT EQUATIONS
The equation for Special Relativity (SR) relative motion-caused radial redshift is not the same, butit gives approximately the same redshifts for small velocities and redshifts; as the speed approaches the speed of light the SR redshift becomes infinite. The equation is (from Wikipedia, but well known from SR chapters in a first intro to SR)
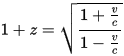
For the Cosmological Redshift, it is different, and in fact spacetime can expand faster than light with a finite redshift. The results comes from the FLRW metric for the universe as (again, from the Wikipedia article)
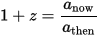
Eq. (1), with a the scale factor, now (when received by us), and then (when emitted)
By the way, note that the definition itself of redshift is the same in all cases, just some simple ratio of observed and emitted frequency or wavelength. From that Wikipedia article redshift is defined equivalently from frequency or wavelength change, since when redshift occurs the c = f$\lambda$, so if one changes the other will change equivalently. the redshift z is defined as
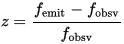
for frequency shift and
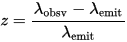
Eq. (2)
for wavelength change, but they are equivalent, and always happen together.
So the rationale for both is what wavelength or frequency is observed, compared to what is emitted.
REDSHIFT IN GENERAL RELATIVITY
In GR it is derived from the metric, setting ds = 0 for the photon path in a radial lightlike geodesic
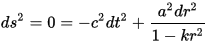
The physics is that one then observes the distance and time between the passing of two consecutive crests (or equal wave phase points). The observed crests' deltas, observed when emitted at t(then), and when received at t(now) [yes, you have to be careful, it is derived in Wikipedia], are different because they are observed at a commoving distance and point where commoving points are further away (in physical distance) from each other due to the expansion of space, ie, the metric physical distances getting larger.
For an observer observing the crest of a light wave at a position r = 0 and time t = t(now), the crest of the light wave was emitted at a time t = t(then) in the past and a distant position r = R. Integrating over the path in both space and time that the light wave travels yields:

Wikipedia then spends some time integrating those and getting the inter-crest distance and time, and the ratio of wavelengths comes out to be
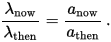
Just substitute in Eq. (2) [with emit = then and obs = now), and you get Eq. (1)
GR REDSHIFT NEAR EARTH
Although I'm not covering the gravitational redshift in other metrics, the redshift as one moves away from the surface of the Earth (it is derived from the Schwarzschild spherically symmetric static GR vacuum solution) is also in that Wikipedia article. It has been accurately observed on the GPS satellites orbiting the earth (yes, there's two effects, a Doppler SR effect and a GR gravity effect, for the GPS satellites the GR effect dominates), and in fact it has to be used to offset that from the GPS clocks so they stay in sync with the standard in Earth.
REFERENCES
See some simple and fun explanations at
https://medium.com/starts-with-a-bang/ask-ethan-39-why-does-light-stretch-as-the-universe-expands-e0a94466e2ba#.d1yjooc70
The math and a more serious explanation and derivation you can find in Wikipedia at https://en.wikipedia.org/wiki/Redshift