Getting energy from decelerating a space-ship

Question

This question comes from another answer.

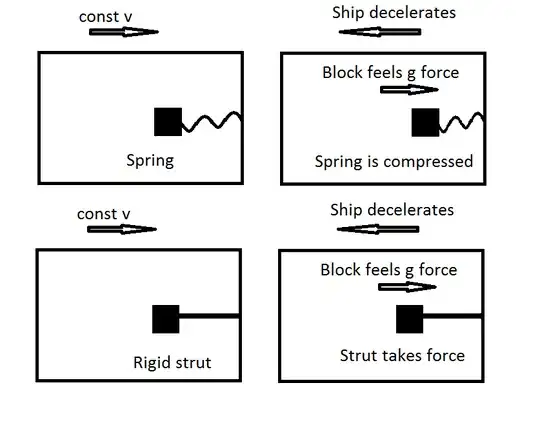
The proposed system is one where the moving space-ship decelerates and some object which is free to move within the ship feels the g forces of this deceleration and imparts this energy to some system (through piezoelectric crystals or however you like, the example I'll use is a spring).

I've been considering it and something didn't quite sit right with me about it but I'm not sure what. It seemed you shouldn't be able to pull energy out...but then maybe this is all force that different parts of the space-ship would feel regardless but the rigid structure would take it rather than a spring. To hopefully make this easier to understand I've illustrated the idea below.

Does it require more energy for the top system to work than the bottom or is the top example making use of forces that would otherwise have been unused? If so, how?

For completeness I should add that part of what lead me to be unsure were the comments below that answer by @HarryJohnston and @sammygerbil, any clarification on their comments would be welcome.

Edit: I think part of what bothered me was that (assuming the spring and strut are the same weight) we should have an equal case in terms of momentum transfer. Taking the ship as one object and providing thrust of equal and opposite momentum to decelerate it would mean that (presumably) both ships stop at the same time because the ship should have 0 net momentum. It may be that the spring is compressing so the outside of the ship is moving a little backwards and the block is moving forwards but together these should have 0 net momentum.

So we're storing energy in the spring despite having the same momentum change where does that come from?

Answer 1

The overall energy is the same before and after deceleration. The spring introduces a delay in the application of deceleration to the internal block.

Further the deformation of the spring will store some energy, which may be released when external deceleration stops. Consequently it takes more energy to decelerate (but you an get some back)

Answer 2

It depends on how "strut takes force"

There are two possibilities how that impact can be absorbed, depending on how one interprets the vague description of "strut takes force". By itself, the diagram is incomplete and unclear because it's not an isolated system, that strut is attached to something and it matters.

Either the strut is anchored to a hypothetical immovable point, and then "strut takes force" means that the strut absorbs the energy either as elastic deformation (i.e. as the first illustration of a spring) or as plastic deformation (i.e. heat) or breaking up and converting the impact into kinetic energy of components of what used to be a strut.

Or, alternatively, the strut is considered to be not deformable (as the infamous spherical cow in vacuum) - so all impact is transferred to whatever (large, heavy) object the strut is attached to, so it can be modeled as a simple elastic collision of two objects.

In either case, if the spaceship arrives at speed v and ends up with speed 0 in the same inertial reference frame, for the energy perspective it doesn't matter how it stops. Energy is conserved; kinetic energy decreases by $mv^2$ so something else increases by $mv^2$, and the only difference is how much of that is transformed to something that is (subjectively) useful to you.

Answer 3

Yes it does require more energy for the top system to work compared to the bottom system.

The exhaust gases of the rockets of the top system are not moving to the right as fast as the exhaust gases of the rockets of the bottom system.

So the top system must produce more of the exhaust gases in order to give the exhaust gases the same momentum as the exhaust gases of the bottom system have.

So to experience the same change of momentum as the bottom system, the top system must burn more rocket fuel.

Answer 4

Consider the forces F1 and F2 that stop both systems with the same constant deceleration, g. F2 = 2mg for the bottom system and it stays that way until the space-ship stops at zero speed. F1 on the other hand starts with a value of mg and as the inner mass contracts the spring more and more, it (F1) gradually increases. Actually when sthe spring has contracted by c, F1 = mg + kc. Contraction stops when kc = mg. Then F1 = mg + mg. If the inner mass finds time to stop at zero during the deceleration, then F1 reachs 2mg eventually. If you plot force-distance graph for F1 and F2 during full deceleration with g, you will see that area under F1 (work done by the force) is LESS than the area under F2.

Inevitably, momentum is conserved in the complete system: ship + the system that applies the decelerating force. Latter part could be the gas propulsion or it could be another spring attached to another mass, say, the earth. It could even be a magnetic field of some magnet with some mass. If the overall system is elastic in both cases, kinetic energy will be conserved beside the momentum. Then the latter system will gain some kinetic energy. This will be equal to the kinetic energy of the space-ship (as it has lost all of its kinetic energy) which is the same for both systems. If that is the case, final total energy of the whole system (again, the space-ship + the system that provides deceleration) will be larger than the kinetic energy of the space-ship by the amount stored by the spring in the top system. For the bottom system total energy will be all kinetic energy and by the definition of elastic collision,the latter system will not spend any more energy. Conclusion is that if the complete system is elastic, there must be energy transfer from the part of the system that provides deceleration for the top system. We don't need this for bottom system.

If the complete system is not required to be elastic, final system will have less kinetic energy for both top and bottom systems. The difference will be converted into heat or some other form of energy in both systems. However, top system will partly convert the difference into potential energy stored in the spring.