1. How can we "interact" with a photon with a purely mechanical device such as a shutter?
Here is the culprit - the QED vertex:
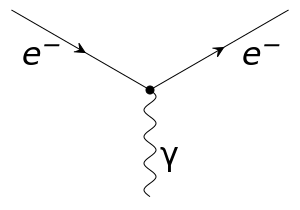
The mechanical shutter, whether made from metal or plastic, contains charged particles (electrons and atomic nuclei). Charged particles interact with photons via the QED vertex. On the most fundamental (and most pedantic) level, this is the mechanism at work.
Thought experiment: try shifting the photon frequency with a shutter made of neutrinos (which do not interact via the QED vertex). It won't work.
2. Draw me a QED diagram responsible for the interaction
The answer may depend on the nature of the shutter. So let's choose the simplest possible "shutter" - a dilute gas of free electrons, whose density is somehow being varied with frequency $\omega_2$. Note that there's no need to block the light completely - any change to the total scattering amplitude will still cause the frequency-shifting effect. Here is the relevant QED diagram:
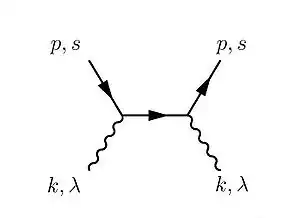
A photon enters with wavevector $(\vec{k_1}, \omega_1)$ and exits with the same wavevector $(\vec{k_1}, \omega_1)$. You can think of this as elastic scattering by angle zero.
3. How can scattering with $\theta = 0$ possibly have any effect?
The zero-angle scattering amplitude interferes quantum-mechanically with the no-scattering amplitude to form the outgoing amplitude at angle zero - see the optical theorem.
4. How can scattering with $\Delta \omega = 0$ possibly have any effect?
Because the scattering amplitude of the photon at frequency $\omega_1$ is being modulated in time with frequency $\omega_2$, which leads to an EM field excitation at $\omega_1 + \omega_2$ - see the convolution theorem.

