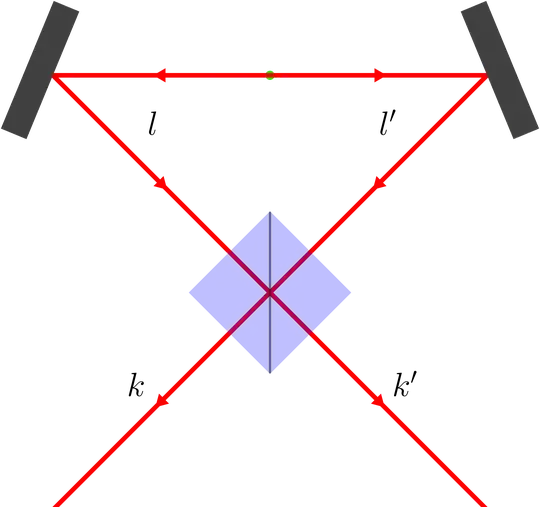
Consider two photons emitted in two different modes $l$ and $l'$ (for instance by the annihilation of an electron and a positron), such that the initial state of the system is $\left|\psi\right\rangle =\left|1_{l}\right\rangle \otimes\left|1_{l'}\right\rangle$ .
Now at some point, I reverse the second photon and put it in the mode $l$ (for instance using a reflection on a mirror to change the direction and polarization of the photon).
What is the good description of the final state ?
Is it a two photons state $\left|2_{l}\right\rangle$ ? But shouldn't the phase between both photons be taken into account so that the interference could be positive or destructive ?
Is it twice a one photon state $\left(1+e^{i\varphi}\right)\left|1_{l}\right\rangle$ ?
Is it something else ?
Does the question make sense ?