Method of image charges for a point charge and a non-grounded conducting plane

Question

I know how to solve Laplace's equation for a point charge in front of a grounded conducting infinite plane. But I want to know what happens (both physics and math) when the infinite conducting plane isn't grounded, or is connected to a potential $V$.

Answer 1

The problem is addressed in Electrodynamics Fulvio Melia Example 2.1 page 39, using Green function techniques. However, I cannot fully understand his final solution. Let us define the plane held at a constant potential $V_0$ to be the $z$-$y$ plane. The charge $q$ is at the distance $a$, namely at $(a,0,0)$. The potential at large distances is zero. The solution (Eq. 2.54) is

$$V(x,y,z) = V_{image} (grounded) + V_0 f(x,y,z).$$

The first term is the usual image method solution, for the case where the conducting plane is grounded, namely

$$V_{image}(grounded) = q\left[\left[(x-a)^2 + y^2 + z^2\right]^{-1/2} - \left[(x+a)^2 + y^2 + z^2\right]^{-1/2}\right],$$

which gives zero when $x=0$. In other words this is the solution of the Poisson equation, but the boundary conditions are not those required.

The second term, $V_0 f(x,y,z)$ is the solution of Laplace equation, and $f(x,y,z)$ is $V_0$ independent.

According to the text book Eq. (2.54) there

$$f(x,y,z) = (x/2 \pi) \int dz' \int dy' \left[x^2 + (y-y')^2 + (z-z')^2\right]^{-3/2}.$$

The integrals over the primed variables stretch from minus infinity to plus infinity and this function is V_0, q and the length scale a independent.

The solution is mysterious for me. Namely, we can get rid of $y$ and $z$ in the integral (for any finite $y$ and $z$) by change of variables of integration. Then the integral can be solved (for $x>0$) and the solution is $f(x,y,z)= x/ x = 1$. Well, that is wrong (or subtle) since that would mean that we only need to add to the usual image solution a constant $V_0$. This does not satisfy the boundary condition at large distances from the plane where the potential is zero.

Maybe the integral for the dimensionless function f(x,y,z) should be regularised somehow.

Since the image part of the solution, $V_{image}(grounded)$, takes care of the charge in the Poisson equation, we can find a solution that is a linear combination of $V_{image}(grounded)$ and some other function, the latter solves the Laplace equation. Then let the boundary at $x=L$ be grounded and we want to take $L\to \infty$ and on x=0 we have V_0 (this seems like a legitimate trick). The Laplace equation for this problem gives
$$V(x,y,z) = -V_0 x/L + V_0,$$ and if we take $L\to \infty$ we get the result just mentioned (for any finite $x$) namely a constant (which does not satisfy the boundary condition at infinity). So I think the limit of a large system ($L\to \infty$) is creating a certain non-trivial problem, which ultimately is related to the Green function technique used by Fulvio Melia. Any ideas?

Of-course if f(x,y,z) is unity for any finite distance x, this would mean that switching from grounded plane to non-grounded one (compared to zero potential at infinity) has practically no effect. This hypothesis was postulated in some of the previous discussions.

Answer 2

If you would like to define V at infinity as zero and the conducting plane as not grounded, you can also think of the solution as a superposition of two different elctrostatic cases: Take the fields expression of a single charge and a grounded plane, and sum this with the fields given off by a plane of fixed potential.

Answer 3

I also think that there would be a difference between the two situations. Lets take a non-grounded PEC plane and say a positive charge lies above it. The field created by the charge will induce negative charges to be stacked on the top (towards the positive charge) of the PEC, and since there is no creation nor destruction of charge, the same and opposite charge will be induced on the bottom surface of the PEC. In this way, treating the thickness of the PEC as infinitely small, both induced surface charges cancel each other over large distances, as seen by the positive charge. In this way, nothing changes in respect to the field generated around the positive charge (since the PEC as no total charge). Though, if the PEC is grounded, it acts like an infinite source of charges that can be arranged in any way, dictated by the surrounding charges. So the positive charge induces an electric field on the upper surface of the grounded PEC, BUT no charge on the lower surface since charge must not be conserved in this situation (that is what ground means!). We are then left with a charge that as electric field lines pointing towards the PEC, all coming at right angles with the latter. This situation is exactly equal to a dipole made of the same positive charge, and a equal negative charge situated an equal distance normal to the PEC.

Answer 4

When we ground the conductor what we are doing is essentially removing the effect of positive charge induced. But if we do not ground it we have to take account of the positve charge induced too.

We can say the effect of induced negative charge(only) is roughly same as when the conductor was grounded so we assume a $-q$ charge at distance d. from surface(on which -ve charge is induced). If we assume charge distribution of $-q$ and $+q$ to be symmetrical we can similarly place $+q$ charge at a distance d from the surface where +ve charge is induced.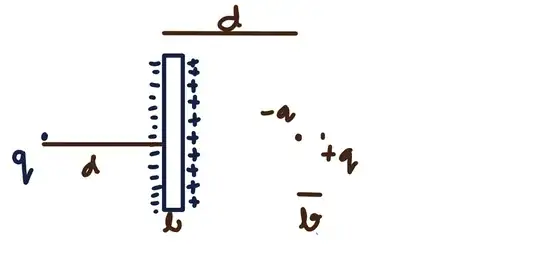

Note: This is just an approximation.

Answer 5

I'm responding to the May 13 2021 post by Eli Barkai -- which is a very nice post so many thanks to Eli for an insightful post. And many thanks to Alireza for bringing this nice question up. My perspective on his quandry: the INFINITELY large "conductive plane" that extends to infinity causes mathematical complexity because a) electrical charge can be harvested from an INFINITELY large number of locations along this plane, which thus acts as "grounding" because charge can be brought in from infinitely far away (but still along the plane), and b) any attempt to uniformly spread charge on the plane will cause voltage to be non-zero at infinite distances from the plane.

Therefore it seems this problem can only be formulated as 1) a non-infinitely large conducting plane that is non-grounded and can have its voltage modified, or 2) an infinitely large conductive plane that is grounded and cannot have its voltage modified.

For case 1, the large-yet-finite-sized conductive-foil will have the same charge distribution from the famous original "image method" solution PLUS it can be put to any additional voltage by spreading additional charge uniformly around it's surface.

For case 2, ANY attempt to modify the voltage of the infinite-plane will cause voltage at infinity to be nonzero thus invalidating the problem description.

Answer 6

If the problem you're trying to solve only contains one point charge and the conducting infinite plane at potential V, then there is no physical difference between the plane's potential being 0 (grounded) or +V, because the electric potential may be globally shifted by a constant value everywhere...