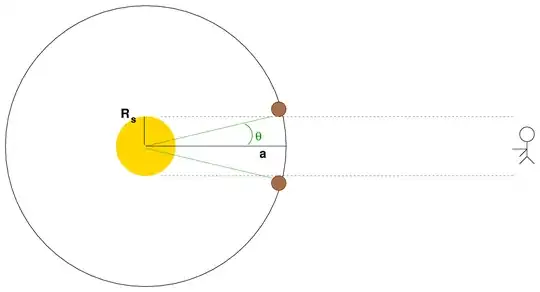
Given that we are at a random orientation to any remote star system, it seems to me that there is only a narrow angle at which transits of exoplanets can be observed.
Imagine a large mathematical sphere with the remote system at the center, and the Earth on the surface. There would be a belt on that sphere where transits could be observed. Assuming an even probability of our position on that sphere, the chance of us being able to observe a transit would be the ratio of the area of that "transit-observing" belt and the total area of the sphere.
A quick calculation tells me that the probability of being in position to see a transite $P_t$ is almost equal to radius of the star / radius of the planet's orbit ($R_{orbit}=a$).
$$ P_t \approx \frac {R_{star}}{R_{orbit}} $$
Assumptions:
- Distance to star >> $R_{star}$
- Exoplanet is a point. In reality it is non-zero, but this just simple blurs the edge case.
If true, the chance of far observers seeing Earth transits of the sun: $\frac {0.696 \space million \space km}{149.6 \space million \space km} \approx \frac12\% $
The coincidence that we are in position to see the planets in the Trappist 1 system: $\frac {0.114 \cdot 0.696 \space million \space km}{0.011 \cdot 149.6 \space million \space km} \approx 5\% $