Difference between magnetic and electric fields

Question

I need to understand the concept on how to distinguish between electric fields and magnetic fields. For example, if a negatively charge particle enters the region with a velocity of 7 m/s east and two seconds later has a velocity of 11 m/s, 44 degrees South of East, then my question is what type of field in what direction is in the region and how can I tell this for sure? Let's assume that the regions have either a uniform electric or magnetic field present.

Answer 1

Magnetic force acting on a charged particle can never change the kinetic energy of the particle because whenever a particle enters a UNIFORM magnetic field, the component of magnetic field along the velocity won't exert any force and the component perpendicular to the velocity can only change the direction of the particle but not it's speed.

$\vec{F}=q\vec{v}\times \vec{B}$

$|\vec{F}|=q|\vec{v}| |\vec{B}| \sin\theta$

As you can see, any component of the uniform magnetic field parallel to (or along) the velocity, cannot exert any force because $\theta =0, \sin0 = 0$.

And the component of the magnetic field perpendicular to the velocity can exert force as $\sin{90}=1$ but the work done by this force will be zero because $\cos\theta$ becomes $0$. Therefore, this force cannot alter the particle's kinetic energy.

$W=|\vec {F}||\vec{d}|\cos\theta$

On the other hand force by the electric field can do that.

$\vec{F}=q\vec{E}$

This force can change the direction as well as the magnitude of the velocity.

In your case, both the magnitude and the direction of velocity are changing. Thus, it has to be an electric field.

Answer 2

Magnetic force is cross product of charge×velocity and magnetic field. Hence a magnetic force is always perpendicular to velocity. A force perpendicular to velocity only changes its direction.

So the field is electric field as the velocity is increasing.

So if velocity increase it is electric field and if only direction changes it is magnetic field.

Answer 3

I need to understand the concept on how to distinguish between electric fields and magnetic fields.

Note the Wikipedia electromagnetic field article : "Over time, it was realized that the electric and magnetic fields are better thought of as two parts of a greater whole — the electromagnetic field". An electron doesn't have an electric field or a magnetic field, it has an electromagnetic field. Also see what Minkowski said in Space and Time:

"In the description of the field caused by the electron itself, then it will appear that the division of the field into electric and magnetic forces is a relative one with respect to the time-axis assumed; the two forces considered together can most vividly be described by a certain analogy to the force-screw in mechanics; the analogy is, however, imperfect".

The electorn has an electromagnetic field, and electromagnetic field interactions result in linear electric force and rotational magnetic force. When we only see the former we talk of an electric field, when we only see the latter we talk of a magnetic field. There's a magnetic field around the current-in-the-wire because the linear forces cancel but the rotational forces don't.

For example, if a negatively charge particle enters the region with a velocity of 7 m/s east and two seconds later has a velocity of 11 m/s, 44 degrees South of East, then my question is what type of field in what direction is in the region and how can I tell this for sure?

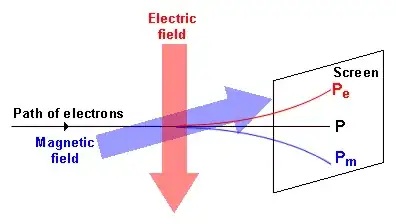
There's not enough information here. Take a look at this picture of electron deflection from The Electronic Science Tutor by Georges Delpierre and Trevor Sewell:

You can contrive your electric and magnetic fields to deflect your electrons one way or another.

Let's assume that the regions have either a uniform electric or magnetic field present.

I don't like that assumption for various reasons. And I don't think it helps anyway. What you need is a further measurement of the particle motion to distinguish between linear and rotational force.