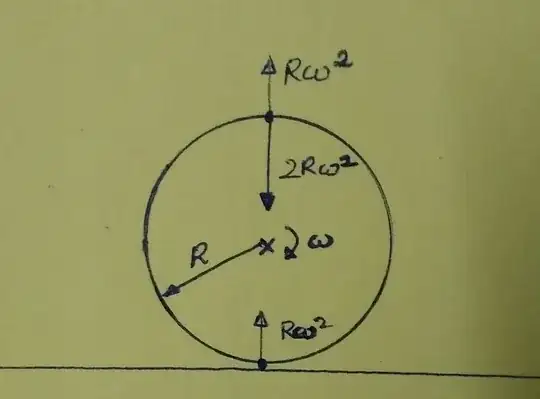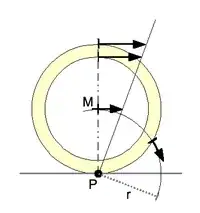
A purely rolling wheel of radius $R$, has its ICOR at the point $P$ (as per the figure).
If I calculate the centripetal force on a particle at the top most point of the rim, considering point $P$ as its center of rotation, I get the value of the force to be $F=2mR \omega^2$, where $\omega$ represents angular velocity.
If I calculate the force using the radius of curvature of cycloid, I end up with the value of $F=mR\omega^2$, which is indeed true.
My concern is that why doesn't ICOR provide me with the correct answer.