The special theory of relativity angle contradiction

Question

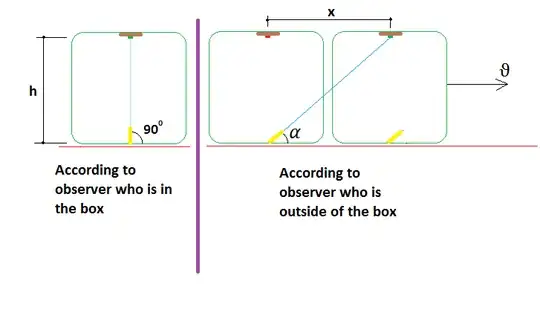
I always see this picture for proof of the time relation between frames that moves relatively constant speed in the special theory of relativity.

The time for the observer who is in the box which travel at constant speed $V$.

$$ t'=\frac{h}{c} \tag 1$$

The time for observer who is outside of the box.

$$ t=\frac{\sqrt{x^2+h^2}}{c} \tag 2$$

$$ t=\frac{x}{V} \tag 3$$ and the time relation between observers is $$ t'=t \sqrt {1-\frac{V^2}{c^2}} \tag 4$$ Everything is Ok till here.

According to outside observer, the person who adjusts the laser gun (yellow drawn in picture) angle in the box must change the angle ($\alpha$) as shown in right side of the picture if the light is not affected from the speed of the box as the special theory of relativity claims. However, According to inside observer who adjust the laser angle, the angle should be exactly $90^0$ because the inside observer will not understand that the box moves.

How does the special theory of relativity explain this dilemma?

(Please assume that the sensor on top is very small and the laser has very focused slim light beam and the box is quite speedy otherwise the angle always would be very near $90^0$ and the angle cannot be detected for low speeds. )

Answer 1

The laser gun is not rotated for the outside observer. It is still at 90 degrees. Just imagine that some laser light leaks out of the back of the laser gun, then you would have two different angles that the laser gun would have to rotate in ....

The laser gun is still at 90 degrees relative to the box but it sends out light under an angle because of non-simultaneity. The phase over the surface of its output is not constant in the x-direction due to non-simultaneity. Such a varying phase is also how phased array radars can send out a beam under an angle. See the image below (source: https://en.wikipedia.org/wiki/Phased_array)

It sends out the beam under an angle and the wavefront of the laser beam also rotates (The wave front should always be in the direction of the propagation). See the middle image below for the Lorentz transformed frame.

The image at the left depicts a photon bouncing up and down in the box for the observer inside the box. The middle image shows the photon bouncing up and down as seen by the observer outside the moving box.

Without non-simultaneity, as in the "Mansoury-Sexl" transform in the image on the right, the wavefront would not rotate.

The image below explains the effect. The term $~t' =\gamma(t-\beta x)~$ shows how $t'$ depends on x. Looking at the image below: At the left side time has progressed further and thus the phase of the wave front has progressed further. At the right side it's the opposite. The net effect is that the wavefront rotates.

For more see the relevant chapter of my book here: http://www.physics-quest.org/Book_Chapter_Non_Simultaneity.pdf

Answer 2

From the point of view of the outside observer the laser gun should not be tilted. It will be directed straight up too. The source and photon will move in positive x direction with the same velocity and will always have the same x coordinate. Please look at this video:

https://www.youtube.com/watch?v=5-AAC4pemDI

In the first episode moving source (a lamp) launches a photon. Both photon and the lamp always have the same X coordinate. Then a small tube appears on the top of the lamp. This tube imitates laser pointer, which always directed at right angle to direction of motion.

I think I understand what confuses you. You think that for moving observer velocity of light in different directions is the same. Not quite. Imagine two observers A and B, who move relatively to each other. Let A conduct observations from his reference frame K. A admits, that velocity of light is c in his frame K. But, if observer B, who moves in this frame K flashes a lamp, observer A will see, that light recedes from B with different velocities in different directions.

However, if B wants to conduct measurements, he introduces his own frame K’ and admits that velocity of light in different directions is c. But now B will see, that if A flashes a lamp, light recedes from A with different velocities.

In Special Relativity observer NEVER admits state of his own motion. Observer is always at rest in his own rest frame.

Thus, in Special Relativity every observer covers “mutual for all observers” space by his own reference frame. This reference frame implies that there is an Einstein – synchronized clock in each point of space. Special Relativity is the change of frames. Observers never use one mutual one, but each has his own.

In the same frame moving observer sees, that clock of observer at rest runs faster, not slower. If he wants to measure time dilation, he has to change reference frame and introduce his own one.

Please compare how many ticks moving clock does and how many any synchronized one. Moving clock makes less ticks that one at rest. That means, from the point of view of a moving clock time in reference frame tick faster. You will see, that once moving clock turns into one at “rest” so as to see time dilation.

https://en.wikipedia.org/wiki/Time_dilation#/media/File:Time_dilation02.gif