1

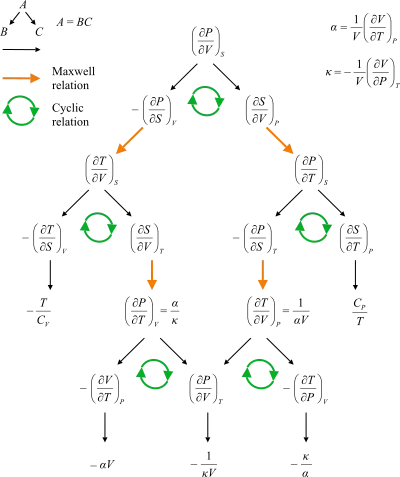
I am just learning about partial differentiation and Maxwell relations cropped up as an example. Considering that we are dealing with the 4 different variables $p$, $V$, $S$ and $T$. I would think that there would be 6 Maxwell relations because when using the Legendre transformations, there are 6 choices of two variables from these 4 for me to create a function dependent on these two variables. And I thought that this would mean there are 6 relations. Try as I might I cannot seem to find any more than the four that are given in my lecture notes.

When I looked this up, Wikipedia stated that

... the four most common Maxwell relations are the equalities of the second derivatives of each of the four thermodynamic potentials, with respect to their thermal natural variable (temperature $T$; or entropy $S$) and their mechanical natural variable (pressure $P$; or volume $V$)...

which seems to imply that there are more than four. However, the graph on the same Wikipedia page

enter image description here

Picture from Wikipedia.

This makes it look like there are only 4 non-degenerate ones?

Qmechanic
  • 220,844
Meep
  • 4,167

2 Answers2

3

It's funny that you have fallen in the same mistake I made when studying Maxwell relations just a few weeks ago. At first glance, it may look that the total number of Legendre transforms has to be $C^2_4$ which is equal to $6$.

However, not every combination is possible, T and S are always coupled in the same term and so are P and V. Therefore, the total number of combinations becomes $$A^2_2 \times A^2_2=4$$

Tofi
  • 2,699
-2

Aren't there 64 relations? At least that's what I recall from when I was doing my eng-phys undergrad at McMaster

Dimitrios
  • 1