1

I imagined a theoretical experiment about gravity. First of all, I know that it is very hard to build such sensitive test apparatus with our current technology but it is just theoretical experiment to enlighten the general relativity.

Let's imagine, We have a big perfect sphere balloon whose inner side of the surface is covered with light detecting sensors. There is one laser on center that can send laser beam to any direct from the center of the sphere. Laser beam hits the sensors that are placed the inner side of the balloon surface. Thus, the test apparatus can measure 2 angles in sphere coordinates both laser direction in center and the hit point on surface. We can calculate a curve equation from hit points of the laser lights via changing diameter of the balloon for any direction.

Could you please help me what we would observe if we build such test apparatus?

My Questions:

  1. What should be the curve equations while the balloon is fixed on earth ?

  2. Arrival time of the laser light to the surface from the center will be same or different, If we test all directions?

  3. If we release the balloon in free fall , what would happen about the arrival time to surface and curve equations? (My estimation All direction of laser lights will behave as if there was no any mass in universe because of the general relativity equivalence principle for free fall.(Is it true?). Will the curve equations turn into line equation for each direction? )

  4. Imagine that we know the whole curve equations to any direction and arrival time to surface for the direction when it is fixed on earth? Can we calculate the major mass via these curve equations? How?

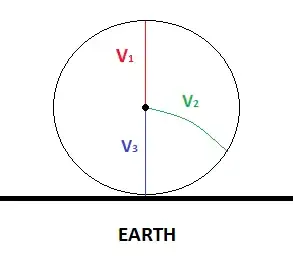
    EDIT: enter image description here

After @John Rennie's answer, I had got more questions. The subject became more interesting for me. I would like to add some more questions. If we test laser in 3 directions as shown in picture. (Please consider only Earth's gravity effect )

I wonder what the trajectory speeds of light for 3 directions would be? (I mention$|\vec{ V_1(t)}|$,$|\vec{ V_2(t)}|$,$|\vec{ V_3(t)}|$)

  • $|\vec{ V_1(0)}|=|\vec{ V_2(0)}|=|\vec{ V_3(0)}|=c_0$ ? where $c_0$ is the speed of the light in air.
  • If we compare the trejectory speeds after t , what we would say about $|\vec{ V_1(t)}|,|\vec{ V_2(t)}|,|\vec{ V_3(t)}|?$

And what can say about arrival times to surface? ($t_1,t_2,t_3$)

Community
  • 1
Mathlover
  • 541

1 Answers1

4

Your apparatus seems to be just a complicated way of asking if light travels in a straight line at constant speed, and the answer is that it only does so if spacetime is flat. More precisely, your experiment tests if spacetime is locally flat i.e. flat to within experimental error over the length scale of your experiment.

Suppose you are far from any massive bodies so spacetime is flat and you are floating weightless. Then the spacetime geometry is described by the Minkowski metric and light travels in a straight line at constant speed.

Now suppose you are still far from any massive bodies but someone has sneaked up and attached a rocket motor to your spacesuit so you experience some constant acceleration $a$. Now your spacetime is described by the Rindler metric. In this case light doesn't (generally) move in straight lines and it doesn't move at a constant speed.

Now let's put you close to a massive body like the Earth. Suppose you are falling freely, like the astronauts in the International Space Station, so you are weightless. In this case your spacetime is locally flat and in your local vicinity light will travel in a straight line at constant speed. I'm using the term locally because even though you are weightless, if you look far enough from your position you'll find there are tidal forces and these will cause the light to curve. But keep the distances small enough that tidal forces aren't significant and your experiment will measure the light travelling in straight lines at constant speed.

And finally let's put you standing stationary on the surface of the Earth. Now you are experiencing a constant acceleration (of $g$ i.e. 9.81 m/s${}^2$) just as when we attached a rocket motor to your spacesuit. So in this case you will measure the trajectory of the light to be curved and the speed of the light to change with position.

The point of all this is that if you are doing a local measurement then all you need to consider is your proper acceleration i.e. the acceleration you experience measured in your rest frame. If and only if this acceleration is zero will you measure light to travel in a straight line at constant speed.

John Rennie
  • 367,598