Compressible material with Poisson ratio of 0.5

Question

According to comments and an answer to this question, it is claimed that:

1. Incompressible materials require the Poisson ratio to be 0.5.
2. A poisson ratio of 0.5 does not imply that the material is incompressible.

It is thus implied that the statement "A material has a Poisson ratio of 0.5 if and only if the material is incompressible" is false, and that causality cannot be reversed. However, the maths seem reversible, and I have not been able to find any compressible material with a Poisson ratio of 0.5, whether that be in practice or theory.

Note: arguably only theory matters; the hypothesis is academic: no real material exists with a Poisson ratio of exactly 0.5.

Can above second statement be proven with theoretical evidence (e.g. by presenting a theoretical material with a Poisson ratio of exactly 0.5 that does change volume for small stress/strain)? Or, alternatively, can the second statement be disproven mathematically (e.g. by proving reversibility of causality)?

Answer 1

Idealized liquids have a Poisson's ratio of exactly 1/2 and are not incompressible (because no material is incompressible). No solid can have a Poisson's ratio of exactly 1/2.

To explain: If you apply a deviatoric (i.e., not hydrostatic; the 1-D version is shear) load on a liquid, it will deform without resistance and without a change in volume, implying that $\nu=1/2$. One way to see this is to use one of the elasticity relations (which assume a homogeneous isotropic linear elastic material): $G=\frac{3K(1-2\nu)}{2(1+\nu)}$. All stable materials have a positive bulk modulus $K$ (i.e., all stable materials compress to some degree under hydrostatic stress); thus, setting $\nu=1/2$ implies a shear modulus $G$ of zero, which corresponds to a fluid.

Let's look at a couple of the elasticity relations from the Poisson's ratio side: $\nu=\frac{3K-E}{6K}$, where $E$ is the Young's elastic modulus, and $\nu=\frac{3K-2G}{2(3K+G)}$. Thus, elastomers have a Poisson's ratio of nearly 1/2 because their shear and Young's elastic moduli are much smaller than their bulk moduli. When you shear or pull on rubber, for example, it's relatively easy to unkink and uncoil its long polymer chains to obtain shearing or uniaxial deformation. When you apply pressure from all sides, however, you're essentially trying to push C atoms closer to C atoms, which is not easy.

Note that this review (Greaves et al., "Poisson’s ratio and modern materials", Nat Materials 10 2011, DOI: 10.1038/NMAT3134) defines $\nu=\frac{3K-2G}{2(3K+G)}=0$ for gases for unexplained reasons, possibly because they are idealizing gases as exhibiting $K=0$.

Answer 2

Poisson's ratio can be described using longitudinal speed of sound and shear speed of sound.

$$ν=\frac{1}{2}\cdot(cL^2-2\cdot cS^2)/(cL^2-cS^2 )$$

$ν$ is Poisson's ratio, $cL$ is longitudinal speed of sound and $cS$ is shear speed of sound

Solids support shear, ideal liquids cannot support shear, so the $cS$ terms go to zero and the $cL/cL = 1$, thus $ν=1/2$.

Answer 3

Start with an unconstrained (circular) rod of an isotropic material. Apply a longitudinal tension stress. The relative change is volume $dV/V_o$ of the rod can be derived as below with Poisson's ratio $\nu$ and transverse strain $\epsilon_a$.

$$ \frac{dV}{V_o} = \nu^2\epsilon_a^3 + \left(\nu^2 - 2\nu\right)\epsilon_a^2 + \left(1 - 2\nu\right)\epsilon_a $$

An incompressible material is one that does not change volume as it is deforms when subjected to stress. Volume conservation in an isotropic material is $dV/V_o = 0$. Formulations using the bulk modulus show that the requirement can be fulfilled when $\nu = 1/2$.

Plot the relative volume versus strain as below.

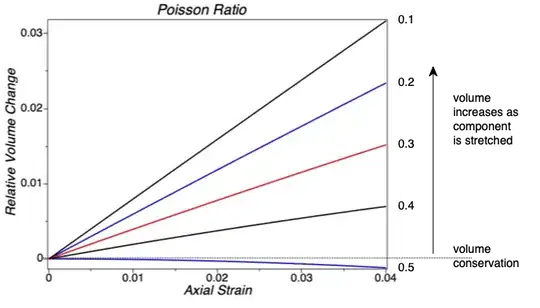
We see that isotropic materials that have $\nu \neq 0.5$ do not conserve volume as they are stretched. We see that even isotropic materials with $\nu = 1/2$ only conserve volume in the limit $\epsilon_a \rightarrow 0$. Interestingly, isotropic materials with $\nu = 1/2$ will shrink in volume when subject to longitudinal tension stress.

We can appreciate from this graph why cork $\nu \approx 0$ is a better material in a bottle of wine than using natural rubber $\nu \approx 0.5$. Pulling or pushing on cork longitudinally will cause almost no change in radius

$$ \frac{dV}{V_o} = \frac{dl}{l_o} + 2\frac{dr}{r_o} \approx \epsilon_a = \frac{dl}{l_o} \Rightarrow \frac{dr}{r_o} \approx 0$$

The natural rubber will by comparison have

$$ \frac{dr}{r_o} \approx \frac{1}{2}\frac{dl}{l_o}$$

meaning that it will be easier to remove from the wine bottle (it shrinks in radius as it is pulled out) but more difficult to re-insert back (it expands in radius as it is compressed back into the bottle).

In summary:

• The assumption of incompressibility is equivalent to stating that $\nu = 1/2$ for an isotropic material under isotropic pressure.

• Even if an isotropic material has $\nu = 1/2$, its volume is not conserved when it is subject to any level of anisotropic strain deformation.

The derivation of an expression for $dV/V_o$ for an anisotropic material likely demands the use of tensor notation. I leave this reference as a starting point for further enjoyment as desired.