Free electron theory of metals works unreasonably well in spite of the fact that we neglect the Coulomb repulsion between the electrons. Is there deeper reason why this should work? Somewhere I heard that this has to do something with Fermi liquid theory but I'm not familiar with it. Can someone explain in simple terms why free electron theory works? The underlying explanation should also be able to guess situations where it should expected not work.
2 Answers
In simple terms, the reason that free electron theory works is that the (non-interacting) electrons in a metal form a fermi-surface. If in the absence of interactions the fermi surface is the ground state of the system.
If you add coulomb interaction this will enable electrons to interact. However, due to the Pauli exclusion principle (and conservation of momentum) there are very few electrons that actually are capable of scattering against each other. Basically since there is a Fermi surface only electrons close to the at the edge of the surface can actually scatter.
The tendency to scatter also goes to zero, as one approaches the Fermi surface from the outside. This vanishing tendency to scatter means that excitations of the non-interacting fermions are almost a correct description of the excitation also in the interacting case.. as long as you are close to the Fermi surface (and we typically are).
As to when this picture fails, is for instance the case of superconductivity. If there are small attractive (instead of repulsive) interactions between the electrons, this destabilizes and destroys the fermi-surface, invalidating the whole picture.
- 3,967
The free electron model was introduced before quantum mechanics theory of solids was developed. The following shows what happens to the electrons bound in a solid state lattice
The whole lattice is involved in the formation of the bands, there is no individual identity to the electrons, they just occupy the available energy levels in each band, while as fermions they also obey the Pauli exclusion principle: one electron at each energy level.
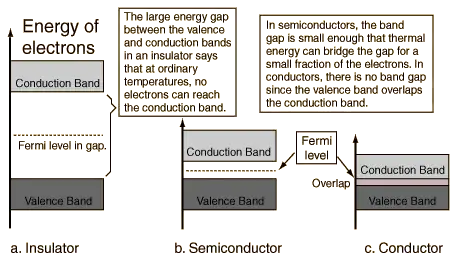
An important parameter in the band theory is the Fermi level, the top of the available electron energy levels at low temperatures. The position of the Fermi level with the relation to the conduction band is a crucial factor in determining electrical properties.
Most solid substances are insulators, and in terms of the band theory of solids this implies that there is a large forbidden gap between the energies of the valence electrons and the energy at which the electrons can move freely through the material (the conduction band).
The electrons bound in the valence band cannot move freely unless energy excites them into the conduction band, where their mobility is through the whole lattice, no longer bound in around a specific nucleus . The difference between insulators and conductors lies in the energy necessary for the transition from the valence band to the conduction band. In insulators it is large, in metals it is very small, and the transition energy is available from the black body radiation, the vibrations of the lattice. Thus in the conduction band they are as free.
It should be noted that coulomb interactions are already included in the quantum mechanical boundary value problem of "electrons in lattice", for the qualitative solution shown in the image above.