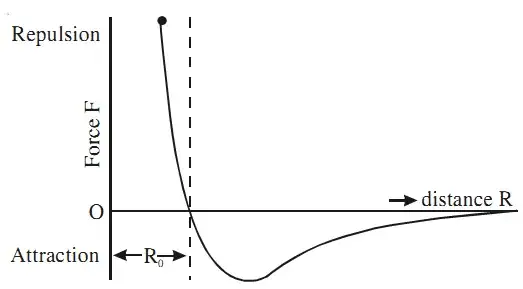
The most typical example of such a potential is the Lennard-Jones potential:
$$ V = -\left(\frac{r_0}{r}\right)^6+\left(\frac{r_0}{r}\right)^{12}$$
This is repulsive at very short distances, but attractive at large distances, as you said in your question. In fact the Lennard-Jones potential is a mathematically simple guess based on these assumptions.
But why do we expect such behaviour? Even though an atom or a molecule is electrically neutral overall, the charge might be distributed unevenly (you can think of it as having a positively charged and a negatively charged part). This uneven distribution may be due to quantum fluctuations for atoms, or to the molecular structure for molecules. Anyways, it gives rise to a dipole moment, usually called $p$, which in turn produces an electric field $E \propto p/r^3$. Now, this field will induce a dipole moment $p'$ in another molecule so that $p' \propto E \propto p/r^3$. The potential energy of two dipoles scales like $p p' /r^3$ therefore giving rise to the $1/r^6$ potential.
On the other hand, when two atoms come really close together, two things happen: first of all, the subatomic structure becomes relevant, for instance in the form of electrons in the outer shells repelling each other; another effect which will be relevant is the Pauli exclusion principle, which roughly speaking in this case prevents two particles from occupying the same space. The reason why we pick $12$ as the exponent is probably due to convenience for calculations more than any other physical reason.