When all else fails, do dimensional analysis.
Force: [M1 L1 T-2] /
Area: [M0 L2 T0] =
Pressure: [M1 L-1 T-2] /
Length: [M0 L1 T0] =
Pressure Gradient: [M1 L-2 T-2]
Energy: [M1 L2 T−2] /
Volume: [M0 L3 T0] =
Energy Density: [M1 L-1 T-2] /
Length: [M0 L1 T0] =
Energy Density Gradient: [M1 L-2 T-2]
In point of fact, the highest pressure ever attained by humankind at the time was done by increasing energy density via lasers in fusion experiments.
Yes, pressure and energy density are two forms of the same thing, just as pressure gradient and energy density gradient are two forms of the same thing.
Thus, just as, for instance, water only spontaneously flows down a pressure gradient (ie: downhill), energy only spontaneously flows down an energy density gradient. This is reflected in 2LoT in the Clausius Statement sense.
[EDIT]
https://i.imgur.com/QErszYW.gif

Idealized Blackbody Object (assumes emission to 0 K and ε = 1 by definition):
q_bb = ε σ (T_h^4 - T_c^4) A_h
= 1 σ (T_h^4 - 0 K) 1 m^2
= σ T^4
Graybody Object (assumes emission to > 0 K and ε < 1):
q_gb = ε σ (T_h^4 - T_c^4) A_h
The 'A_h' term is merely a multiplier, used if one is calculating for an area larger than unity [for instance: >1 m^2], which converts the result from radiant exitance (W m-2, radiant flux per unit area) to radiant flux (W).
Temperature is equal to the fourth root of radiation energy density divided by Stefan's Constant (ie: the radiation constant).
e = T^4 a
a = 4σ/c
e = T^4 4σ/c
T^4 = e/(4σ/c)
T = 4^√(e/(4σ/c))
T = 4^√(e/a)
q = ε σ (T_h^4 – T_c^4)
∴ q = ε σ ((e_h / (4σ / c)) – (e_c / (4σ / c))) Ah
Canceling units, we get J sec-1 m-2, which is W m-2 (1 J sec-1 = 1 W).
W m-2 = W m-2 K-4 * (Δ(J m-3 / (W m-2 K-4 / m sec-1)))
∴ q = (ε c (e_h - e_c)) / 4
Canceling units, we get J sec-1 m-2, which is W m-2 (1 J sec-1 = 1 W).
W m-2 = (m sec-1 (ΔJ m-3)) / 4
One can see from the immediately-above equation that the Stefan-Boltzmann (S-B) equation is all about subtracting the radiation energy density of the cooler object from the radiation energy density of the warmer object.
∴ q = σ / a * Δe
Canceling units, we get W m-2.
W m-2 = (W m-2 K-4 / J m-3 K-4) * ΔJ m-3
For graybody objects, it is the radiation energy density differential between warmer object and cooler object which determines warmer object radiant exitance.
Do keep in mind that a warmer object will have higher energy density at all wavelengths than a cooler object:
https://i.sstatic.net/qPJ94.png
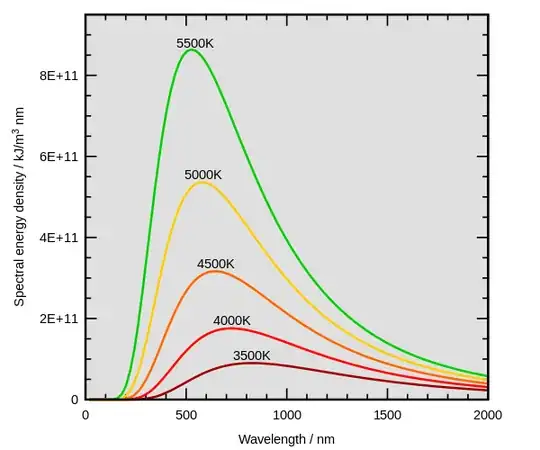
Warmer objects don't absorb radiation from cooler objects (a violation of 2LoT in the Clausius Statement sense and Stefan's Law); the lower radiation energy density gradient between warmer and cooler objects (as compared to between warmer object and 0 K) lowers radiant exitance of the warmer object (as compared to its radiant exitance if it were emitting to 0 K). The radiation energy density differential between objects manifests a radiation energy density gradient, each surface's radiation energy density manifesting a proportional radiation pressure.

