Warp drive with gravitational waves in the nonlinear regime

Question

gravitational waves are strictly transversal (in the linear regime at least), also their amplitudes are tiny even for cosmic scale events like supernovas or binary black holes (at least far away, maybe we should ask some physicists located a bit closer to the center of the galaxy), but lets put all those facts aside for a second and consider a gravitational source big enough to generate gravitational waves with amplitudes of the order of the galaxy. For instance consider a planar wave like in my mediocre drawing:

$$ h_{\alpha \beta} e^{i (k_{y} y - \omega t)} $$

where

$$ h_{\alpha \beta} \approx 1 $$

so the perturbation is in the nonlinear regime

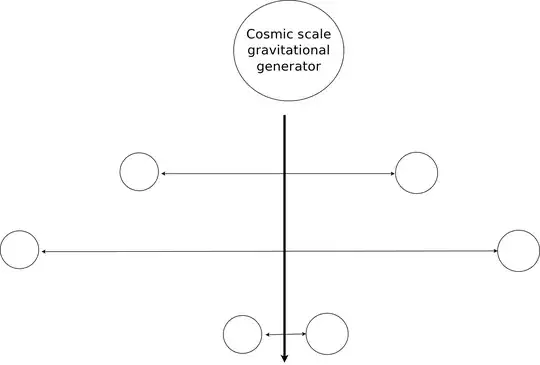
i draw two far away objects in three different time slices (this is why they are repeated 3 times), the topmost is the objects without the gravitational wave, the one in the middle represents the objects in the crest of the gravitational wave, and the one in the bottom represents the objects in the valley of the wave.

So, my point is that people would only have to travel an arbitrarily small distance when the wave is on the valley (assuming circular polarization) even if the "normal" distance (i.e: $h_{\mu \nu} = 0$) is several light-years away

Besides being slightly impractical to set up such a mammoth gravitational source, this kind of warp drive is valid from a physical standpoint? Are there any physical limits to gravitational wave amplitudes in such nonlinear regime?

Answer 1

I don't think you could use this as a warp drive unless you could collimate the gravity waves. If you consider a spaceship moving at constant velocity through a gravity wave, the ship will be accelerated then decelerated again as the wave passed through but it's average velocity would be unchanged. The only way you could get a net effect from the wave is if you could move from a region of high amplitude to low amplitude within half a cycle of the wave. I can't think of any (plausible) geometry that would allow this. Possibly you could do it very close to a black hole binary, where the gravity wave generation doesn't look like a point source.

Answer 2

Here is a paper called Creating spacetime shortcuts with gravitational waveforms

That seems to be close to what you are talking about, but with smaller effects and 'smaller' gravitational wave amplitudes.

What you do is fly your ship so that it only flies through the shrinking part of gravitational waves - so your trip takes place only in the compacted part of some waves which are travelling in a transverse direction to your chosen direction of travel.

So its kinda a big technical stretch - but I think that its actually less audacious than your scheme - it also shows that linear waves will do the kind of effect you are looking for.

As for physical limits on the size of the wave amplitudes you are talking about, remember that the gravitational wave observation of GW150914 had amplitudes close to 1 (well say a tenth) in a region 200 km across or so, and it radiated power at a peak rate of 200 Solar masses per second. So a galaxy sized radiator with amplitudes near 1 would need something like 2 back holes, each the mass of 10 million spiral galaxies merging to get to that power. (I did that 10 million mass calculation rather hastily, feel free to check it. Just make a black hole the size of the Milky Way and see how many solar masses it would take).

Answer 3

A linearized warp drive means considering higher order powers of the shift vector negligible. If $g_{\mu\nu}(\alpha,\beta)$ is a warp drive metric depending on the lapse function $\alpha$, and the shift vector $\beta$, then the approximation is valid

$$g_{\mu\nu}(\alpha,\beta) \approx \eta_{\mu\nu} + h_{\mu\nu}(\alpha,\beta) \,,$$

$\eta_{\mu\nu} = \text{diag}(-1,1,1,1)$ is the Minkowski metric, and $h_{\mu\nu}(\alpha,\beta)$ is a linearized metric with $O(\beta)$ only. Lobo and Visser tried this approach in Linearized warp drive and the energy conditions, and analyzed how it would impact energy conditions. You could check for wave-like solutions for the Einstein equations in this regime.