1

Consider the motion of a sphere which is rolling (without slipping) inside another sphere.

Derive the constraint equations of the rolling condition.

Note

  • This is a 3D rigid body problem. In fact, we are considering a general 3 dimensional motion of sphere inside another sphere.

  • $\alpha$ and $\beta$ are general functions of time and determine the position of the center of the sphere.

My Effort

The constraint equations should follow from the fact that the velocity of the contact point vanishes. So denoting the contact point by $C$ and the center of the sphere by $G$ we should have

$$ \mathbf{v}_C=\mathbf{v}_G+\boldsymbol{\omega}\times \mathbf{r}_{G/C}=\mathbf{0} $$

In order to go further, I need to write $\mathbf{v}_G$ and $\boldsymbol{\omega}$ in term of the angles $\alpha$, $\beta$ and the classic Euler angles. I am stuck here!

Any help is appreciated.

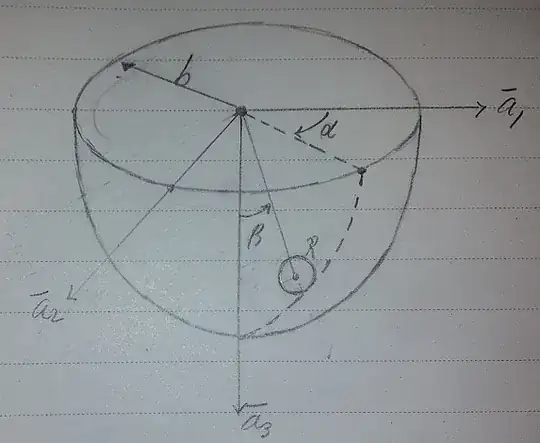
enter image description here

Hosein Rahnama
  • 269

1 Answers1

1

The no slipping conditions adds 3 constraints to the 5 degrees of freedom of the problem. The velocity of the contact point should be zero (as you stated).

$$ \mathbf{v}_C = \mathbf{v}_G + \mathbf{r}_{G/C} \times \boldsymbol{\omega} = 0$$

The position vector $\mathbf{r}_G$ is a function of the angles $\alpha$ and $\beta$ only

$$ \mathbf{r}_G = (b-R) \begin{pmatrix} \cos(\alpha) \sin(\beta) \\ \sin(\alpha) \sin(\beta) \\ -\cos(\beta) \end{pmatrix} $$

By differentiation you get at the linear jacobian $\mathtt{J}_A$ relating the generalized velocities $\dot{q}_A = (\dot{\alpha}, \dot{\beta})$ to the cartesian velocity of the center $\mathbf{v}_G = \mathtt{J}_A \dot{q}_A$

$$\mathbf{v}_G = (b-R) \begin{vmatrix} -\sin\alpha \sin\beta & \cos\alpha \cos\beta \\ \cos\alpha \sin\beta & \sin\alpha \cos\beta \\ 0 & \sin\beta \end{vmatrix} \begin{pmatrix} \dot{\alpha} \\ \dot{\beta} \end{pmatrix} $$

The orientation matrix $\mathtt{E}$ of the ball depends on three Euler angles $\varphi$, $\psi$ and $\theta$ representing rotations about local axes $\mathbf{x}_1$, $\mathbf{x}_2$ and $\mathbf{x}_3$ respectively.

$$ \mathtt{E} = \mathrm{Rot}(\mathbf{x}_1,\, \varphi)\,\mathrm{Rot}(\mathbf{x}_2,\, \psi)\,\mathrm{Rot}(\mathbf{x}_3,\, \theta) $$

Again by differentiation using the chain rule you arrive at the rotational jacobian $\mathtt{J}_B$ relating the generalized rotational velocities $\dot{q}_B = (\dot{\varphi},\dot{\psi},\dot{\theta})$ to the ball rotational velocity $\boldsymbol{\omega} = \mathtt{J}_B \dot{q}_B$

$$ \boldsymbol{\omega} = \mathbf{x}_1 \dot{\varphi} + \mathrm{Rot}(\mathbf{x}_1,\, \varphi)\,\left(\mathbf{x}_2 \dot{\psi} + \mathrm{Rot}(\mathbf{x}_2,\, \psi)\, \mathbf{x}_3 \dot{\theta}\right) $$ $$\boldsymbol{\omega} = \begin{vmatrix} \mathbf{x}_1 & \mathrm{Rot}(\mathbf{x}_1,\, \varphi)\,\mathbf{x}_2 & \mathrm{Rot}(\mathbf{x}_1,\, \varphi)\,\mathrm{Rot}(\mathbf{x}_2,\, \psi)\,\mathbf{x}_3 \end{vmatrix} \begin{pmatrix} \dot{\varphi} \\ \dot{\psi} \\ \dot{\theta} \end{pmatrix} $$

The above jacobian $J_B$ is a 3×3 matrix with the first column $\mathbf{x}_1$, the second column $\mathrm{Rot}(\mathbf{x}_1,\, \varphi)\,\mathbf{x}_2$ etc.

Also note that $\mathbf{r}_{G/C} \times \boldsymbol{\omega}$ can be written in matrix form as $$ \begin{vmatrix} 0 & -z_{G/C} & y_{G/C} \\ z_{G/C} & 0 &-x_{G/C} \\ -y_{G/C} & x_{G/C} & 0 \end{vmatrix} \begin{pmatrix} \omega_x \\ \omega_y \\ \omega_z \end{pmatrix} $$

NOTE: Related answer proving the relationship between Euler angles and rotational velocity

Community
  • 1
John Alexiou
  • 40,139