Different cold dark matter density parameters from early- and late-Universe observations

Question

Edit: @John Rennie, thank you for your good and concise review of how the parameters of the $\Lambda$CDM model evolve with time. However, the answer I was looking for was a different one (sorry for the incorrect and inaccurate formulation of my question).

My second attempt:

The $\Lambda$CDM model, the standard model of cosmology, implies that today's cold dark matter (CDM) density parameter is $\Omega_c=0.2589±0.0057$. Thus, according to the cosmological standard model, CDM makes up $\sim 80\%$ of the current matter density. This is inferred from early-Universe observations, such as the Cosmic Microwave Background (CMB) or the Baryonic Acoustic Oscillations (BAO), and it changes over time (sorry for my inaccurate statement before).

My actual question is: are there local (i.e. late-Universe) observations, for example, from nearby galaxy rotation curves, which give a different $\Omega_c$? I read here that the CDM content of our Milky Way is $95\%$ and here that there are even galaxies made of up to $99.99\%$ of CDM. Therefore, I was wondering whether it would be observationally allowed to have a mechanism leading to additional CDM matter production in the late Universe, so that the $\Lambda$CDM model is only be correct in the early Universe.

As I formulated it in the initial question: would it be in contradiction to any observation to have $\sim 25\%$ of CDM in the early Universe, but up to $\sim 30\%$ in today's Universe (thus created very recently), measured for example by galaxy rotation curves?

Answer 1

The cold dark matter density parameter $\Omega_c = 0.2589 \pm 0.0057$ is not a constant. What you have quoted is the current value of $\Omega_c$ i.e. its value right now.

At at time $t$ the fraction of dark matter will be:

$$ x_{dm}(t) = \frac{\rho_{dm}(t)}{\rho_r(t) + \rho_m(t) + \rho_{dm}(t) + \rho_\Lambda(t)} $$

where $\rho_r$ is the density of relativistic matter (photons and neutrinos), $\rho_m$ is the density of ordinary matter, $\rho_{dm}$ is the density of dark matter and $\rho_\Lambda$ is the density of dark energy. However the various densities do not scale equally with the expansion of the universe. Specifically if $a(t)$ is the scale factor and $\rho_{r0}$ etc mean the current densities then:

$$\begin{align} \rho_r &= \frac{\rho_{r0}}{a^4(t)} \\ \rho_m &= \frac{\rho_{m0}}{a^3(t)} \\ \rho_{dm} &= \frac{\rho_{dm0}}{a^3(t)} \\ \rho_\Lambda &= \rho_{\Lambda0} \end{align}$$

The two forms of matter have densities inversely proportional to volume, as you'd expect. However the relativistic matter density falls as $a^{-4}$ because it has a pressure and it does work as it expands. The density of the dark energy is constant and not dependent of $a(t)$ because it's a property of space.

So if you take the limit of $a \to 0$, i.e. approach the Big Bang, the $a^{-4}$ dependence of $\rho_r$ means it will dominate so $\Omega_r \approx 1$ and $\Omega_m \approx \Omega_{dm} \approx \Omega_\Lambda \approx 0$. Likewise as $a \to\infty$ dark enegy will dominate so $\Omega_\Lambda \approx 1$ and $\Omega_r \approx \Omega_m \approx \Omega_{dm} \approx 0$.

To calculate $\Omega_{dm}$ as a function of time requires a numerical integration as there isn't an analytical solution. However going forward in time $\Omega_{dm}$ will fall as dark energy comes to dominate. Going back in time $\Omega_{dm}$ will rise to a maximum then nearer to the Big Bang it will fall again as the relativistic matter starts to dominate.

Answer 2

The $\Lambda$CDM model, the standard model of cosmology, implies that today's cold dark matter (CDM) density parameter is $\Omega_c=0.2589±0.0057$. Thus, according to the cosmological standard model, CDM makes up $\sim 80\%$ of the current matter density.

No problem. I think most people are fairly happy with that. Well at least I am. Those flat galactic rotation curves aren't there for nothing. Hence we have the dark matter pie:

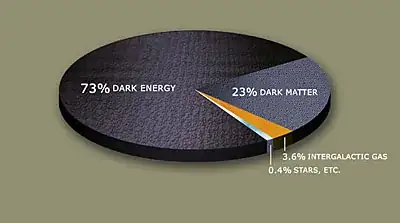
This is inferred from early-Universe observations, such as the Cosmic Microwave Background (CMB) or the Baryonic Acoustic Oscillations (BAO), and it changes over time (sorry for my inaccurate statement before).

Note though that we are dealing with a model rather than hard scientific fact. We don't actually know that ratios change over time. But it's fun to kick this sort of thing around.

My actual question is: are there local (i.e. late-Universe) observations, for example, from nearby galaxy rotation curves, which give a different $\Omega_c$?

I'm not sure they give a different $\Omega_c$ but there are observations which cause issues. See for example Dark Matter Dominates in Nearby Dwarf Galaxy: "The total mass I measured was much, much greater than the mass of the total number of stars—implying that there's a ton of densely packed dark matter contributing to the total mass," Kirby says. "The ratio of dark matter to luminous matter is the highest of any galaxy we know. After I had made my measurements, I was just thinking—wow."

I read here that the CDM content of our Milky Way is $95\%$ and here that there are even galaxies made of up to $99.99\%$ of CDM.

That's what people say: "Motions of the stars tell you how much matter there is, van Dokkum said. “They don’t care what form the matter is, they just tell you that it’s there. In the Dragonfly galaxy stars move very fast. So there was a huge discrepancy: using Keck Observatory, we found many times more mass indicated by the motions of the stars, than there is mass in the stars themselves". But note that the distribution of ordinary matter is not uniform. Why should the distribution of dark matter be uniform? And more to the point, why should the distribution of vacuum energy be uniform? Because the FLRW metric assumes it? I don't know about you, but I don't like assumptions in my science.

Therefore, I was wondering whether it would be observationally allowed to have a mechanism leading to additional CDM matter production in the late Universe, so that the $\Lambda$CDM model is only be correct in the early Universe.

I think so. But only if dark matter is not composed of particulate matter, but is instead spatial energy-density variations. A star is a concentration of energy in the guise of matter that causes gravity in the surrounding space. But note what Einstein said: "the energy of the gravitational field shall act gravitatively in the same way as any other kind of energy". That's a concentration of spatial energy causing gravity in the surrounding space. Check out papers like papers like Inhomogeneous and interacting vacuum energy by Josue De-Santiago, David Wands, Yuting Wang. Think of space as a thing with its vacuum energy, not a nothing. Then say to yourself space expands between the galaxies but not within. So the spatial energy density within a very old galaxy would be high compared to the surrounding space. That energy has a mass-equivalence. It would look like there was a lot of dark matter present. And in case you hadn't noticed, space is dark.

As I formulated it in the initial question: would it be in contradiction to any observation to have $\sim 25\%$ of CDM in the early Universe, but up to $\sim 30\%$ in today's Universe (thus created very recently), measured for example by galaxy rotation curves?

Not that I know of. Note that if the early universe was homogeneous, then the spatial energy density would have been totally uniform and it would look like there was no dark matter at all.