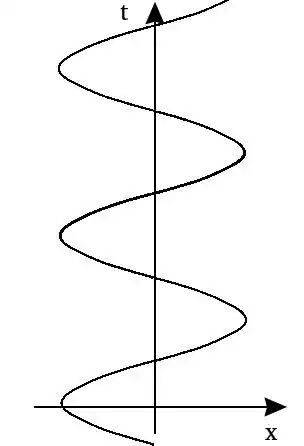
All timelike geodesics that pass through the coordinate origin of AdS (under the standard parameterization) execute simple harmonic motion about the origin with a period proportional to the AdS radius, as discussed at AdS Space Boundary and Geodesics and on Carroll pg. 327. This statement seems to pick out a special point in space about which all orbits oscillate.
But AdS is maximally symmetric and therefore completely homogeneous, so all points must be physically equivalent and anything that appears special about the origin must end up being just an artifact of the choice of coordinates.
How can we reconcile these two facts? The center of a particle's oscillation seems physical and coordinate-independent. How can there be periodic oscillation without the oscillation being centered at any special point? (After all, given a particle trajectory, there is no coordinate-independent sense of an "initial position at $t = 0$" about which it should oscillate.) Would an observer in AdS ever simultaneously observe two test particles oscillating about different points?