Are wormholes really a valid shortcut to distant points in the universe?

Question

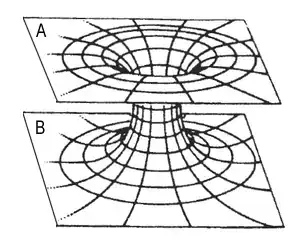
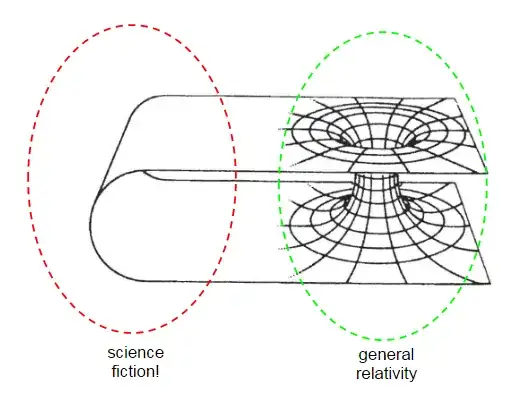
Lately I encountered a few times references to wormholes as a way to reach distant places in the universe in a short time. I have to admit I don't have a proper knowledge of the mathematics behind wormholes (although I won't mind a complete GR explanation in the answer, if necessary). All I know is that wormholes are usually compared to something analogous to a tunnel through the planet Earth to reach distant places in less time. The problem is, if I want to reach the other side of the planet I have to travel 20.000 km on its surface and "only" 12.000 km through its center. While the latter is surely shorter, it's still more than 50% of the initial value and this is the best-case scenario. For shorter distances, the difference becomes more and more negligible.

Now, I know enough of GR to understand that this explanation could be a simplification so extreme that any comparison makes little to no sense, but I'm curious to understand if the same problems arise for wormholes too. I don't really care if wormholes exist, are traversable by spaceships and both the crew and the vessel can survive the travel undamaged, I know they are still a theoretical construct and probably there is more than one formulation for it. What I'm really interested in is:

• How much shorter will the travel be? I'm interested in Earth proper time, because if the reduction is only in the spaceship proper time, the we can achieve the same result "simply" by traveling closer to the speed of light.
• Does the amount of reduction in time depend on the distance between the endpoints? If so, it seems unpractical to travel to near stars through wormholes, if the spacetime geometry of our galaxy doesn't help somehow (local curvature should be higher than global curvature).

Answer 1

Before we get into the issue of travel time we need to point out the science fiction idea of wormholes is rather different to general relativity. There are several kinds of wormhole metrics known in GR, but they just connect two asymptotically flat regions of spacetime. If we use a rubber sheet model it would look something like this:

The wormhole metric tells us the spacetime geometry around the wormhole, but it does not tell us how, if at all, the regions $A$ and $B$ are connected. The usual science fiction idea of a wormhole is something like this:

The green bit of the geometry is described by GR, but the red bit is entirely fanciful. There is nothing in GR to tell us how the two regions $A$ and $B$ might curve round and meet as shown in the second diagram. This is entirely the domain of science fiction.

Your question asks us to compare the time taken by travelling through the wormhole to the time taken for the long way round. The problem is there is no long way round in any of the wormholes known to us, so your question cannot be answered.

However we can calculate the time taken for an observer to pass through the wormhole from region $A$ to region $B$, so we can decide whether wormholes are at least in principle a viable way to travel. But there is one more complication because there are two different definitions of time involved. Suppose you and I start well away from the wormhole, and we both have clocks. You head off through the wormhole while I sit back and wait to see what happens.

I can time your progress with my clock, and this time is called my coordinate time. You can time your progress with your clock and the time you record is called the proper time. The complication is that in general our two times won't agree and in fact they can be wildly different. For example suppose you were jumping into a black hole rather than a wormhole. Your clock would record a finite (and short!) time for you to fall through the horizon and to a messy but quick death at the singularity. However as measured by my clock you would take an infinite time just to reach the event horizon and you would never pass through it. The disagreement between our clocks couldn't be more extreme.

This happens with wormholes as well. Some types of wormholes have a horizon like a black hole so while you pass through the wormhole in a finite proper time I would never see you reach its entrance let alone pass through it. That makes it a pretty useless travel device since you could never go back. Although it's not strictly speaking a wormhole the Reissner-Nordström charged black hole behaves in this way.

But other types of wormhole are much more benign. For example consider the Morris-Thorne wormhole as described in How do spatial curvature and temporal curvature differ?. Not only does this have no horizon, but it's actually pretty boring. If you head towards the wormhole with some initial velocity $v$ then your velocity remains constant and both of us would observe you to pass through the wormhole much as if you were simply travelling in flat spacetime. The time you take to get through depends on the scale of the wormhole, which depends on how much exotic matter we assembled to build it. In principle this time can be made arbitrarily short.

So while we can't answer the question you asked, we can say that for the right sort of wormhole the travel time can be short on everyday timescales. So this wormhole is a perfectly good way for travelling around the universe.